
【题目】如图,在△ABC中,∠BAC=60°,D为AB上一点,连接CD.
(1)如图1,若∠BCA=90°,CD⊥AB,则![]() =______(直接写出结果).
=______(直接写出结果).
(2)如图2,若BD=AC,E为CD的中点,AE与BC存在怎样的数量关系,判断并说明理由;
(3)如图3,CD平分∠ACB,BF平分∠ABC,交CD于F.若BF=AC,求∠ACD的度数.

【答案】(1)![]() ;(2)BC=2AE.理由见解析;(3)∠ACD=40°.
;(2)BC=2AE.理由见解析;(3)∠ACD=40°.
【解析】
(1)根据含30°的直角三角形即可进行求解;
(2)延长AE至F,使EF=AE,连接BF,CF,DF,易证△AEC≌△FED,再证△ABF≌△BAC,即可得到BC=2AE;
(3)在AB上取点G,使AG=AC,易证△ACG为等边三角形,易证△DGC≌△DFB,得∠DBC=∠DCB=∠ACD,即可求出∠ACD=![]() =40°.
=40°.
(1)∵∠BCA=90°,CD⊥AB,∠BAC=60°,
∴AD=![]() ,AC=
,AC=![]()
∴AD=![]()
∴![]() =
=![]()
(2)BC=2AE.理由如下:
延长AE至F,使EF=AE,连接BF,CF,DF,易证△AEC≌△FED,
∴DF=AC=BD,∠EAC=∠EFD,
∴DF∥AC,
∴∠BDF=∠BAC=60°,△BDF为等边三角形,
∴∠DBF=∠BAC=60°,易证△ABF≌△BAC,
∴AF=BC,
∴BC=2AE;

(3)在AB上取点G,使AG=AC,易证△ACG为等边三角形,
∴GC=AC=BF,∠AGC=60°,
∠BFD=∠AGC=60°,易证△DGC≌△DFB,
∴DB=DC,∴∠DBC=∠DCB=∠ACD,
∴∠ACD=![]() =40°.
=40°.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , …按这样的规律进行下去,第2017个正方形的面积为 . 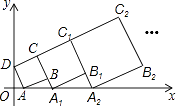
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(-2,1),B(-3,4),C(-1,3),过点(l,0)作x轴的垂线![]() .
.
(1)作出△ABC关于直线![]() 的轴对称图形△
的轴对称图形△![]() ;
;
(2)直接写出A1(___,___),B1(___,___),C1(___,___);
(3)在△ABC内有一点P(m,n),则点P关于直线![]() 的对称点P1的坐标为(___,___)(结果用含m,n的式子表示).
的对称点P1的坐标为(___,___)(结果用含m,n的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得△A1B1C1 , 且点A1落在边AB边上,取BB1的中点D,连接CD,则CD的长为( )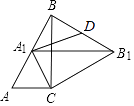
A.![]()
B.![]()
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.设∠BAC=α,∠DCE=β.
(1)如图①,点D在线段BC上移动时,角α与β之间的数量关系是____________,请说明理由;
(2)如图②,点D在线段BC的延长线上移动时,角α与β之间的数量关系是____________,请说明理由;
(3)当点D在线段BC的反向延长线上移动时,请在图③中画出完整图形并猜想角α与β之间的数量关系是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织八年级师生共420人参观纪念馆,学校联系租车公司提供车辆,该公司现有A,B两种座位数不同的车型,如果租用A种车3辆,B种车5辆,则空余15个座位:如果租用A种车5辆,B种车3辆,则有15个人没座位
(1)求该公司A,B两种车型各有多少个座位?
(2)若A种车型的日租金为260元辆,B种车型的日租金为350元辆,怎样租车能使得座位恰好坐满且租金最少?最少租金是多少?(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.
例如:求91与56的最大公约数
解:
请用以上方法解决下列问题:
(1)求108与45的最大公约数;
(2)求三个数78、104、143的最大公约数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com