
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.
例如:求91与56的最大公约数
解:
请用以上方法解决下列问题:
(1)求108与45的最大公约数;
(2)求三个数78、104、143的最大公约数.

【答案】(1)9;(2)13.
【解析】
试题分析:(1)根据题目,首先弄懂题意,然后根据例子写出答案即可;
(2)可以先求出104与78的最大公约数为 26,再利用辗转相除法,我们可以求出26 与 143的最大公约数为13,进而得到答案.
试题解析:(1)108﹣45=63,63﹣45=18,27﹣18=9,18﹣9=9,所以108与45的最大公约数是9;
(2)先求104与78的最大公约数,104﹣78=26,78﹣26=52,52﹣26=26,所以104与78的最大公约数是26;
再求26与143的最大公约数,143﹣26=117,117﹣26=91,91﹣26=65,65﹣26=39,39﹣26=13,26﹣13=13,所以,26与143的最大公约数是13,∴78、104、143的最大公约数是13.


科目:初中数学 来源: 题型:
【题目】一种大米的质量标识为“50±0.25千克”,则下列大米中合格的有( )
A.50.30千克 B.49.70千克 C.50.51千克 D.49.80千克
查看答案和解析>>
科目:初中数学 来源: 题型:
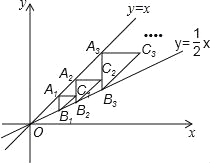
【题目】如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线y=![]() x于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=x和y=
x于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=x和y=![]() x于A2,B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为 .(用含正整数n的代数式表示)
x于A2,B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为 .(用含正整数n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=-3(x-2)2-3可以由抛物线y=-3x2+1平移得到,则下列平移过程正确的是()
A. 先向左平移4个单位长度,再向上平移2个单位长度
B. 先向左平移2个单位长度,再向下平移4个单位长度
C. 先向右平移2个单位长度,再向下平移4个单位长度
D. 先向右平移4个单位长度,再向上平移2个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,属于真命题的是( )
A.相等的角是对顶角B.有两个角是60°的三角形是等边三角形
C.三角形的外角大于任意一个内角D.有三个角分别对应相等的两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各数填在相应的集合里.
(﹣2)2、0 、﹣0. 314、﹣(﹣11)、![]() 、﹣
、﹣![]() 、
、![]() 、|﹣
、|﹣![]() |、10.01001000100001…、
|、10.01001000100001…、![]()
正有理数集合:{__________ …}无理数集合:{__________ …}
整数集合:{__________ …}负分数集合:{__________ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O直径为8cm,有M、N、P三点,OM=4cm,ON=8cm,OP=2cm,则M点在________,N点在圆________,P点在圆________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市现有两种用电收费方法:
分 时 电 表 | 普通电表 | |
峰时(8:00—21:00) | 谷时(21:00到次日8:00) | 电价0.52元/度 |
电价0.55元/度 | 电价0.35元/度 | |
小明家所在的小区的电表都换成了分时电表,根据情况回答下列问题:
(1)第一季度小明家用电情况为:谷时用电量100度,峰时用电量300度,这个季度的费用和用普通电表收费相比,哪种收费方法合算?试说明理由.
(2)一月份小明家用电100度,那么小明家使用分时电表是不是一定比普通电表合算?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com