
分析 (1)根据积的乘方以及同底数幂的乘法即可求出答案.
(2)根据实数运算法则即可求出答案
(3)根据多项式乘以多项式法则以及单项式乘以多项式法则即可求出答案.
(4)根据平方差公式以及完全平方公式即可求出答案.
解答 解:(1)原式=2x6•x3-27x9+25x2•x7
=2x9-27x9+25x9
=0
(2)原式=-8-4+($\frac{1}{2}$×23×1)2
=-12+16
=4
(3)原式=2a2-ab+4ab-2b2-2a2-4ab
=-ab-2b2
(4)原式=[(2x+3y)(2x-3y)]2
=(4x2-9y2)2
=16x4-72x2y2+81y4
点评 本题考查学生的计算能力,解题的关键是熟练运用运算公式,本题属于基础题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
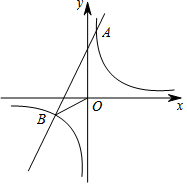 如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).
如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
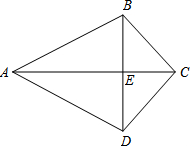 如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.
如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com