
| A. | 不论x取何值,分式都有意义 | B. | 分式的值可以等于1 | ||
| C. | 不论x取何值,分式值都不为0 | D. | 当x=0或-1时,分式无意义 |
科目:初中数学 来源: 题型:填空题
 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为3$\sqrt{2}$,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是14.
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为3$\sqrt{2}$,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是14.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:$\sqrt{3}$,AB=10米,AE=15米.(i=1:$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比)
如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:$\sqrt{3}$,AB=10米,AE=15米.(i=1:$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2•a3=a6 | B. | a8÷a4=a4 | C. | 3a+$\sqrt{2}$a=3$\sqrt{2}$a | D. | (a-b)2=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
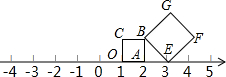 已知正方形OABC,BEFG,按照如图所示位置摆放在数轴上,点O、A、E表示的数分别为1、2、3,若以O为圆心,OF为半径作圆弧,则与数轴的交点表示的数为$\sqrt{10}+1$、-$\sqrt{10}+1$.
已知正方形OABC,BEFG,按照如图所示位置摆放在数轴上,点O、A、E表示的数分别为1、2、3,若以O为圆心,OF为半径作圆弧,则与数轴的交点表示的数为$\sqrt{10}+1$、-$\sqrt{10}+1$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
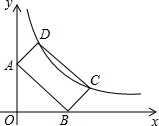 如图,已知矩形ABCD的两点C、D在反比例函数y=$\frac{k}{x}$的图象上,点A和点B都在坐标轴上,且B的坐标为(1,0),AB=2BC,则k=$\frac{3}{4}$.
如图,已知矩形ABCD的两点C、D在反比例函数y=$\frac{k}{x}$的图象上,点A和点B都在坐标轴上,且B的坐标为(1,0),AB=2BC,则k=$\frac{3}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com