
 如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:$\sqrt{3}$,AB=10米,AE=15米.(i=1:$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比)
如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:$\sqrt{3}$,AB=10米,AE=15米.(i=1:$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比)分析 (1)在Rt△ABH中,由tan∠BAH=$\frac{BH}{AH}$=i=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.得到∠BAH=30°,于是得到结果BH=AB.sin∠BAH=10.sin30°=10×$\frac{1}{2}$=5;
(2)在Rt△ABH中,AH=AB.cos∠BAH=10.cos30°=5$\sqrt{3}$,在Rt△ADE中,tan∠DAE=$\frac{DE}{AE}$,即tan60°=$\frac{DE}{15}$,得到DE=15$\sqrt{3}$,如图,过点B作BF⊥CE,垂足为F,求出BF=AH+AE=5$\sqrt{3}$+15,于是得到DF=DE-EF=DE-BH=15$\sqrt{3}$-5,在Rt△BCF中,∠C=90°-∠CBF=90°-45°=45°,求得∠C=∠CBF=45°,得出CF=BF=5$\sqrt{3}$+15,即可求得结果.
解答 解:(1)在Rt△ABH中,
∵tan∠BAH=$\frac{BH}{AH}$=i=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
∴∠BAH=30°,
∴BH=AB.sin∠BAH=10.sin30°=10×$\frac{1}{2}$=5.
答:点B距水平面AE的高度BH是5米;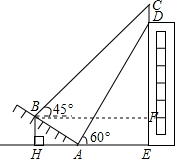 (2)在Rt△ABH中,AH=AB.cos∠BAH=10.cos30°=5$\sqrt{3}$,
(2)在Rt△ABH中,AH=AB.cos∠BAH=10.cos30°=5$\sqrt{3}$,
在Rt△ADE中,tan∠DAE=$\frac{DE}{AE}$,
即tan60°=$\frac{DE}{15}$,∴DE=15$\sqrt{3}$,
如图,过点B作BF⊥CE,垂足为F,
∴BF=AH+AE=5$\sqrt{3}$+15,
DF=DE-EF=DE-BH=15$\sqrt{3}$-5,
在Rt△BCF中,∠C=90°-∠CBF=90°-45°=45°,
∴∠C=∠CBF=45°,
∴CF=BF=5$\sqrt{3}$+15,
∴CD=CF-DF=5$\sqrt{3}$+15-(15$\sqrt{3}$-5)=20-10$\sqrt{3}$≈20-10×1.732≈2.7(米),
答:广告牌CD的高度约为2.7米.
点评 本题考查了仰角、坡度的定义,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:选择题
 如图,在扇形OAB中,∠AOB=90°,半径OA=2,将扇形OAB沿过点B的直线折叠,使点O恰好落在弧AB上的点D处,折痕为BC,则图中阴影部分的面积是( )
如图,在扇形OAB中,∠AOB=90°,半径OA=2,将扇形OAB沿过点B的直线折叠,使点O恰好落在弧AB上的点D处,折痕为BC,则图中阴影部分的面积是( )| A. | π | B. | π-$\frac{2\sqrt{3}}{3}$ | C. | π-$\sqrt{3}$ | D. | π-$\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15.3×104人 | B. | 1.53×105人 | C. | 1.53×106人 | D. | 15.3×105人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
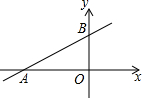 如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )| A. | x>-3 | B. | x<-3 | C. | x>3 | D. | x<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不论x取何值,分式都有意义 | B. | 分式的值可以等于1 | ||
| C. | 不论x取何值,分式值都不为0 | D. | 当x=0或-1时,分式无意义 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com