
【题目】如图,在一正方形ABCD中,E为对角线AC上一点,连接EB、ED.

(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,若∠DEB=150°.求∠AFE的度数.
【答案】(1)证明见解析;(2)65°.
【解析】
试题分析:(1)由正方形的性质得出CD=CB,∠DCA=∠BCA,根据SAS即可得出结论;
(2)由全等三角形的对应角相等得出∠DEC=∠BEC=70°,然后根据对顶角相等求出∠AEF,根据正方形的性质求出∠DAC,最后根据三角形的内角和定理即可求出结果.
试题解析:(1)∵四边形ABCD是正方形,
∴CD=CB,∠DCA=∠BCA,
在△BEC和△DEC中,
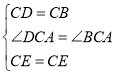 ,
,
∴△BEC≌△DEC(SAS);
(2)由(1)得△BEC≌△DEC,
∴∠DEC=∠BEC=![]() ∠DEB=70°,
∠DEB=70°,
∴∠AEF=∠BEC=70°,
∵四边形ABCD是正方形,
∴∠DAC=45°,
∴∠AFE=180°-70°-45°=65°.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,直角梯形OABC中,AB∥OC,点A坐标为(0,6),点C坐标为(3,0),BC=![]() ,一抛物线过点A、B、C.
,一抛物线过点A、B、C.
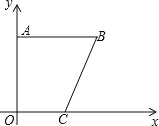
(1)填空:点B的坐标为 ;
(2)求该抛物线的解析式;
(3)作平行于x轴的直线与x轴上方的抛物线交于点E、F,以EF为直径的圆恰好与x轴相切,求该圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2的图像向下平移1个单位。则平移后的二次函数的解析式为( )
A. y= (x-1)2 B. y=(x+1)2 C. y= x2 -1 D. y= x2 +1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织初三社会实践活动,为300名学生每人发了一瓶矿泉水,但浪费现象严重,为此该校环保小组对矿泉水的浪费情况进行抽样调查,并对所发矿泉水喝的情况进行统计,大致可分为四种:
A、全部喝完;
B、喝剩约![]() ;
;
C、喝剩约一半;
D、开瓶但基本未喝.
同学们根据统计结果绘制成如下两张不完整的统计图,根据统计图提供的信息,解答下列问题:
(1)本次调查了 名学生,在图(2)中D所在扇形的圆心角是 度.
(2)请补全条形统计图.
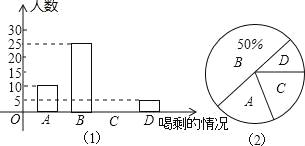
(3)请估计这次社会实践活动中浪费的矿泉水(开瓶但基本未喝算全部浪费,500ml折合为一瓶)约有多少瓶?(保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间x(时)变化的图象(全程)如图所示.有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人都跑了10千米;③甲比乙先到达终点;④两人都跑了20千米.其中正确的说法有( )
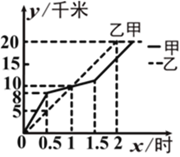
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
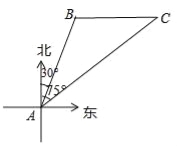
【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
![]()
![]() (参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com