练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

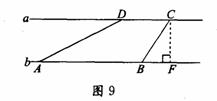
    如图9，河流两岸a，b互相平行，C，D是河岸a上间隔50 m的两根电线杆．某人在河岸b上的A处测得∠DAB＝30°，然后沿河岸走了100 m到达B处，测得∠CBF ＝60°，求河流的宽度CF的值．(结果精确到个位)


    43 m  


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    在△ABC中，∠C=90°，tanA=，△ABC的周长为60，那么△ABC的面积为（  ）

        A．60        B．30       C．240        D．120

    查看答案和解析>>

    科目：初中数学 来源： 题型：


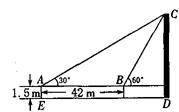
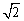    如图，为了测量某建筑物CD的高度，测量人员先在地面上用测角仪AE自A处测得建筑物顶部C的仰角是30°，然后在水平地面上向建筑物前进42 m，此时自B处测得建筑物顶部C的仰角是60°，已知测角仪的高度始终是1.5 m，则该建筑物CD的高度约为_______m(结果保留到1m，参考数据：≈1.4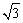，≈1.7)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


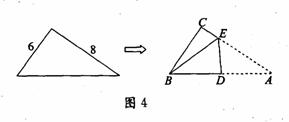
    直角三角形纸片的两直角边长分别为6，8，现将△ABC如图4那样折叠，使点A与点B重合，折痕为DE，则tan∠CBE的值是                                (    )

           A.

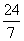
           B.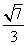

           C.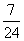

           D.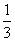

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     如图6所示，小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°，则广告牌的高度BC为        米(精确到0.1米)．(sin35°≈0．57,

    cos35°≈0.82，tan35°≈0.70；sin52°≈0.79，cos52°≈0.62，tan52°≈1.28)

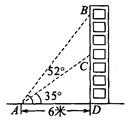
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某地连续四天每天的平均气温分别是：1℃，－1℃，0℃，2℃，则平均气温中最低的是

    A、－1℃  　 　 B、0℃ 　　　　  C、1℃  　　　　　 D、2℃

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     解方程，去分母后，正确的是

    A．                   B． 

    C．                  D．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


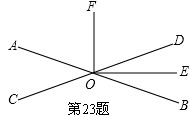
    .如图，两直线AB，CD相交于点O，已知OE平分∠BOD，且∠AOC：∠AOD=3：7，

    （1）求∠DOE的度数；(5分)

    （2）若∠E0F是直角，求∠AOF的度数。（3分）

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    题目“某幼儿园给小朋友分苹果，若每人分3个则剩1个；若每人分4个则差2个。求苹果有多少个？”，解答时设共有x个苹果分给小朋友，列出的方程可以是(  )

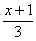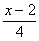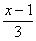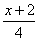        A. 3x＋4=4x－2     B.=     C. =      D.  =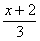

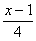
    查看答案和解析>>

    同步练习册答案