
【题目】如图,△ABC中,∠C=90°,AC=6,AB=10,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为 . 
【答案】![]()
【解析】解:过点O作OE⊥AB于点E,OF⊥BC于点F. ∵AB、BC是⊙O的切线,
∴点E、F是切点,
∴OE、OF是⊙O的半径;
∴OE=OF;
在△ABC中,∠C=90°,AC=6,AB=10,
∴由勾股定理,得BC=8;
又∵D是BC边的中点,
∴S△ABD=S△ACD ,
又∵S△ABD=S△ABO+S△BOD ,
∴ ![]() ABOE+
ABOE+ ![]() BDOF=
BDOF= ![]() CDAC,即10×OE+4×OE=4×6,
CDAC,即10×OE+4×OE=4×6,
解得OE= ![]() ,
,
∴⊙O的半径是 ![]() ,
,
故答案为 ![]() .
.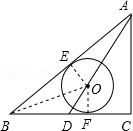
过点O作OE⊥AB于点E,OF⊥BC于点F.根据切线的性质,知OE、OF是⊙O的半径;然后由三角形的面积间的关系(S△ABO+S△BOD=S△ABD=S△ACD)列出关于圆的半径的等式,求得圆的半径.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号种选择:
污水处理器型号 | A型 | B型 |
处理污水能力(吨/月) | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,第一个正方形的顶点A1(﹣1,1),B1(1,1);第二个正方形的顶点A2(﹣3,3),B2(3,3);第三个正方形的顶点A3(﹣6,6),B3(6,6)按顺序取点A1,B2,A3,B4,A5,B6…,则第12个点应取点B12,其坐标为( )

A. (12,12) B. (78,78) C. (66,66) D. (55,55)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E. 
(1)求∠BCE的度数;
(2)若⊙O半径为3,求BE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=﹣ ![]() 的图象与线段AB交于M点,且AM=BM.
的图象与线段AB交于M点,且AM=BM. 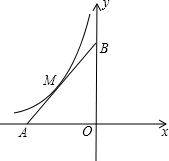
(1)求点M的坐标;
(2)求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
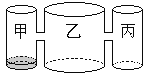
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一个种植总面积为540 m2的长方形塑料温棚,分垄间隔套种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物的总垄数不低于10垄,又不超过14垄(垄数为正整数),它们的占地面积、产量、利润分别如下:

(1)若设草莓共种植了x垄,请说明共有几种种植方案,分别是哪几种;
(2)在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com