
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.  B.
B.  C.
C.  D.
D. 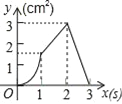
【答案】C
【解析】试题分析:首先根据正方形的边长与动点P、Q的速度可知动点Q始终在AB边上,而动点P可以在BC边、CD边、AD边上,再分三种情况进行讨论:①0≤x≤1;②1<x≤2;③2<x≤3;分别求出y关于x的函数解析式,然后根据函数的图象与性质即可求解.
解:由题意可得BQ=x.
①0x1时,P点在BC边上,BP=3x,
则△BPQ的面积=![]() BPBQ,
BPBQ,
解y=![]() 3xx=
3xx=![]() x2;故B选项错误;
x2;故B选项错误;
②1<x2时,P点在CD边上,
则△BPQ的面积=![]() BQBC,
BQBC,
解y=![]() x3=
x3=![]() x;故D选项错误;
x;故D选项错误;
③2<x3时,P点在AD边上,AP=93x,
则△BPQ的面积=![]() APBQ,
APBQ,
解y=![]() (93x)x=
(93x)x=![]() x
x![]() x2;故C选项错误.
x2;故C选项错误.
故选A.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】为了了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,结果如下:
月用水量(吨) | 10 | 13 | 14 | 17 | 18 |
户 数 | 2 | 2 | 3 | 2 | 1 |
(1)计算这10户家庭的平均月用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是药品研究所测得的某种新药在成人用药后,血液中的药物浓度y(微克/毫升)随用药后的时间x(小时)变化的图象(图象由线段OA与部分双曲线AB组成).并测得当y=a时,该药物才具有疗效.若成人用药4小时,药物开始产生疗效,且用药后9小时,药物仍具有疗效,则成人用药后,血液中药物浓度至少需要多长时间达到最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:

(1)a= ,b= ,c= ;
(2)这个几何体最少由 个小立方体搭成,最多由 个小立方体搭成;
(3)当d=2,e=1,f=2时,画出这个几何体的左视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 对顶角相等 B. 过任意一点可作已知直线的一条平行线
C. 两点之间线段最短 D. 过一点有且只有一条直线与已知直线垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2-4x+7与y=
x2-4x+7与y=![]() x交于A、B两点(点A在点B左侧).
x交于A、B两点(点A在点B左侧).
(1)求A、B两点坐标;
(2)求抛物线顶点C的坐标,并求△ABC面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过A(-1,0)、B(3, 0)、C (0 ,3)三点。
经过A(-1,0)、B(3, 0)、C (0 ,3)三点。
(1)求抛物线的函数关系式;
(2)在抛物线上存在一点P,使△ABP的面积为8,请求出点P的坐标.
(3)在抛物线的对称轴上是否存在一点Q,使得QC+QA最短?若Q点存在,求出Q点的坐标;Q点不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com