
【题目】如图,抛物线![]() 经过A(-1,0)、B(3, 0)、C (0 ,3)三点。
经过A(-1,0)、B(3, 0)、C (0 ,3)三点。
(1)求抛物线的函数关系式;
(2)在抛物线上存在一点P,使△ABP的面积为8,请求出点P的坐标.
(3)在抛物线的对称轴上是否存在一点Q,使得QC+QA最短?若Q点存在,求出Q点的坐标;Q点不存在,请说明理由.

【答案】(1) ![]() ; (2)
; (2) ![]() ; (3)存在,(3)Q(1,2)
; (3)存在,(3)Q(1,2)
【解析】试题分析:(1)因为抛物线![]() 经过与x轴的两个交点A(-1,0),
经过与x轴的两个交点A(-1,0),
B(3,0),所以可设二次函数解析式为![]() ,将C (0 ,3)代入可求
,将C (0 ,3)代入可求![]() ,所以二次函数解析式为
,所以二次函数解析式为![]() .
.
(2)因为AB=4, △ABP的面积为8,根据三角形面积可求得高为4,则点P的纵坐标是4,-4,
令![]() ,可得:
,可得: ![]() ,解得x的值,即点P的横坐标,
,解得x的值,即点P的横坐标,
(3) 在抛物线的对称轴上找一点Q,使得QC+QA最短,根据二次函数图象的对称轴性可得:点A,B关于对称轴对称,连接BC,BC与对称轴的交点即为点Q,利用待定系数法求出直线BC的解析式,再求直线与对称轴的交点.
解:(1)∵二次函数y=ax+bx+c过点A(-1,0),B(3,0),C(0,3)
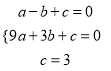 ,解得:
,解得: 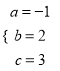 ,
,
∴二次函数的解析式: ![]() .
.
(2)AB=4,
设△ABP的高为h,
∵△ABP的面积为8,
∴![]() AB·h=8,
AB·h=8,
解得:h=4,
当y=4时, ![]() ,
,
解得:x=1,
∴![]()
当y=-4时, ![]() ,
,
![]()
∴![]()
(3)Q(1,2)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.  B.
B.  C.
C.  D.
D. 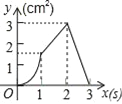
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学习了“圆心角、弧、弦的关系”,实际上我们还可以得到“圆心角、弧、弦、弦心距之间的关系”如下:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距(弦心距指从圆心到弦的距离,如图1中的OC、OC′,弦心距也可以说成圆心到弦的垂线段的长度)中有一组量相等,那么它们对应的其余各组量也相等.请直接运用圆心角、弧、弦、弦心距之间的关系解答下列问题:
如图2,O是∠EPF的平分线上一点,以点O为圆心的圆与角的两边分别交于点A、B、C、D.

(1)求证:AB=CD;
(2)若角的顶点P在圆上,上述结论还成立吗?若不成立,请说明理由;若成立,请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】支付宝与“快的打车”联合推出优惠,“快的打车”一夜之间红遍大江南北,据统计,2016年“快的打车”账户流水总金额达到147.3亿元,147.3亿用科学记数法表示为( )
A.1.473×1010
B.14.73×1010
C.1.473×1011
D.1.473×1012
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店将某种商品按进货价提高100%后,又以6折优惠售出,售价为60元,则这种商品的进货价是( )
A.120元
B.100元
C.72元
D.50元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式能用平方差公式计算的是( )
A. (-x-y)(x-y)B. (2x+y)(2y-x)C. (x-2)(x+1)D. (y-1)(1-y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A. x1=1,x2=-1 B. x1=1,x2=2 C. x1=1,x2=0 D. x1=1,x2=3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com