Question

【题目】如图，在△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，交AB于点E．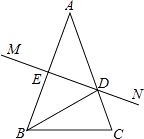
（1）求证：△ABD是等腰三角形；
（2）若∠A=40°，求∠DBC的度数；
（3）若AE=6，△CBD的周长为20，求△ABC的周长．

Answer 1

【答案】
（1）证明：∵AB的垂直平分线MN交AC于点D，

∴DB=DA，

∴△ABD是等腰三角形；

（2）解：∵△ABD是等腰三角形，∠A=40°，

∴∠ABD=∠A=40°，∠ABC=∠C=（180°﹣40°）÷2=70°

∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°；

（3）解：∵AB的垂直平分线MN交AC于点D，AE=6，

∴AB=2AE=12，

∵△CBD的周长为20，

∴AC+BC=20，

∴△ABC的周长=AB+AC+BC=12+20=32．

【解析】（1）根据线段的垂直平分线到线段两端点的距离相等即可得证；（2）首先利用三角形内角和求得∠ABC的度数，然后减去∠ABD的度数即可得到答案；（3）将△ABC的周长转化为AB+AC+BC的长即可求得．
【考点精析】认真审题，首先需要了解线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等)．