
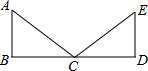
 如图,AB⊥BD,AB∥ED,AC=EC,要证明△ABC≌△EDC,若以“AAS”为依据,还要添加一个条件为∠A=∠E(或∠ACB=∠ECD).
如图,AB⊥BD,AB∥ED,AC=EC,要证明△ABC≌△EDC,若以“AAS”为依据,还要添加一个条件为∠A=∠E(或∠ACB=∠ECD). 分析 根据两角及其中一个角的对边对应相等的两个三角形全等进行判断即可.
解答 解:添加:∠A=∠E(或∠ACB=∠ECD)
∵AB⊥BD,AB∥ED,
∴∠B=∠D=90°,
在△ABC和△EDC中,
$\left\{\begin{array}{l}{∠B=∠D}\\{∠A=∠E}\\{AC=EC}\end{array}\right.$,
∴△ABC≌△EDC(AAS).
故答案为:∠A=∠E(或∠ACB=∠ECD).
点评 本题主要考查了全等三角形的判定,解题时注意:选用哪一种方法,取决于题目中的已知条件,若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12xy2 | B. | 24x2y2 | C. | ab | D. | 12xy |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠CAB=90°,AC=AB,过点A的直线交BC于点M,过点C作CD⊥AM,垂足为D,过点B作BE⊥AM,垂足为E,请你在图中找出一对全等三角形,并说明理由.
如图,在△ABC中,∠CAB=90°,AC=AB,过点A的直线交BC于点M,过点C作CD⊥AM,垂足为D,过点B作BE⊥AM,垂足为E,请你在图中找出一对全等三角形,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
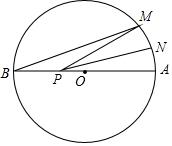 如图,AB是⊙O的直径,AB=6,点M在⊙O上,∠MBA=20°,N是$\widehat{MA}$的中点,P是直径AB上的一动点,若AN=1,则△PMN周长的最小值为( )
如图,AB是⊙O的直径,AB=6,点M在⊙O上,∠MBA=20°,N是$\widehat{MA}$的中点,P是直径AB上的一动点,若AN=1,则△PMN周长的最小值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 按要求完成下列各小题.
按要求完成下列各小题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com