
����Ŀ����ƽ��ֱ������ϵ�У�������![]() ��x�ύ��A��B��A����B�����ࣩ��y�ύ�ڵ�C��
��x�ύ��A��B��A����B�����ࣩ��y�ύ�ڵ�C��
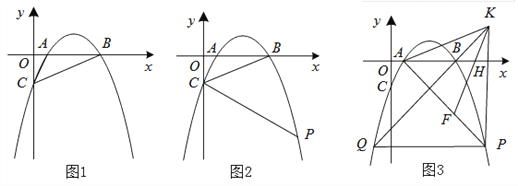
��1����ͼ1������AC��BC�����ABC�������
��2����ͼ2��
�ٹ���C��CR��x�ύ�������ڵ�R�����R�����ꣻ
�ڵ�PΪ����������������һ�㣬����PC������BCP=2��ABCʱ�����P�����ꡣ
��3����ͼ3���ڣ�2��������������F��AP�ϣ�����P��PH��x����H�㣬��K��PH���ӳ����ϣ�AK=KF����KAH=��FKH��PF=![]() ������KB���ӳ����������ڵ�Q����PQ�ij���
������KB���ӳ����������ڵ�Q����PQ�ij���
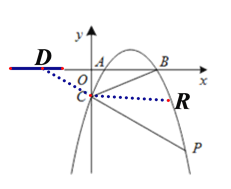
���𰸡���1��3��2����Q��-2��5����6��3��7
����������������1����y=0����![]() =0���õ�A��B�����꣬��x=0�����C�����꣬Ȼ����������������ʽ�����ABC�������
=0���õ�A��B�����꣬��x=0�����C�����꣬Ȼ����������������ʽ�����ABC�������
��2������CR��x���֪��R����������-2����R��q��-2������R��q��-2��������κ�������ʽ���������R�����ꣻ���������֪������PCR=��BCRʱ����P������. �ӳ�PC��x���ڵ�D,����DOC�ա�BOC�����D�����꣬�������ֱ��CD�Ľ���ʽ��Ȼ���������κ���������һ�κ�������ʽ���������P�����ꣻ
��3����FG��PK����֤����HAP=��KPA����HA=HP������AKH�ա�KFG���ɵ�KH=FG=2�������ó�K�����꣬���ɴ���ϵ�������ֱ��KB�Ĺ�ϵʽ��������κ�����ϵʽ���������������Ľ⣬���PQ��x�ἴ�ɵó���.
��⣺��1����y=0����![]() =0��
=0��
��֮�ã�
x1=1,x2=4,
��A(1,0)��B��4.0��;
��x=0�ã�
![]() ��
��
��C��0��-2��.
�� ![]() =3
=3
��2���� �� CR��x��
�� ����R��q��-2��
��![]()
��ã�q1=0��q2=5
�� R��-2��5��
�ڵ���PCR=��BCRʱ����P������
�ӳ�PC��x���ڵ�D,
�� CR��x��,
���PDB=��PCR.
�ߡ�ABC=��BCR=��PCR,
���PDB=��ABC.
�֡�OC=OC����DOC=��BOC=90��,
���DOC�ա�BOC,
��OD=OB,
��D��-4,0��,
��yCD=![]() ,
,
�ⷽ���飺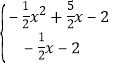 �ã�
�ã�
![]() ��
��![]() ,
,
�� ��P�������6 ;
��3������F��FG��PK�ڵ�G��
�� AK=FK
�� ��KAF=��KFA
����KAF=��KAH+��PAH����KFA=��PKF+��KPF��
��������KAH=��FKP��
���HAP=��KPA��
��HA=HP��
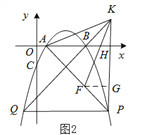
���AHPΪ����ֱ��������
���FPG=45��
���FPGΪ����ֱ��������
��FG=PG=![]() =2
=2
�ڡ�AKH�͡�KFG��
�ߡ�AHK=��KGF=90�㣬��KAH=��FKG��KA=FK
���AKH�ա�KFG��AAS��
��KH=FG=2
��K��6,2��
�� �� B��4,0��
��yKB=x-4
�ⷽ����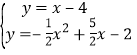 ��
��![]() ��
��![]()
��Q��-1��-5��
��P��6��-5��
��PQ��x��
��PQ=7


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���![]() ͼ����x�ύ��A��B�������Գ���Ϊֱ��x=2�����н�������abc>0�� ��4a+b=0��������A����Ϊ(1��0)�����߶�AB=5�� ������M(x1��y1)��N(x2��y2)�ڸú���ͼ������������0<x1<1��2<x2<3����y1<y2������ȷ���۵����Ϊ�� ��
ͼ����x�ύ��A��B�������Գ���Ϊֱ��x=2�����н�������abc>0�� ��4a+b=0��������A����Ϊ(1��0)�����߶�AB=5�� ������M(x1��y1)��N(x2��y2)�ڸú���ͼ������������0<x1<1��2<x2<3����y1<y2������ȷ���۵����Ϊ�� ��
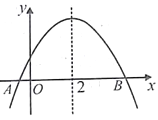
A. ������ B. ������ C. ������ D. ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
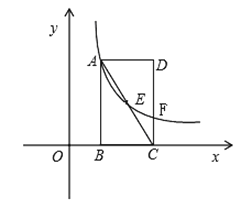
����Ŀ����ͼ, ��ֱ������ϵ�У�������ABCD�ı�BC��X���ϣ���B��D������ֱ�ΪB��1��0����D��3��3��.
��1��ֱ��д����A����C�����꣺A: C: ��
��2��������������![]() ��ͼ��ֱ��AC�ϵĵ�E���ҵ�E������Ϊ��2��m������
��ͼ��ֱ��AC�ϵĵ�E���ҵ�E������Ϊ��2��m������![]() ��ֵ�������������Ľ���ʽ��
��ֵ�������������Ľ���ʽ��
��3������2���еķ�����������ͼ����CD�ཻ�ڵ�F������ EF�����߶�AB�ϣ��˵���⣩��һ��P��ʹ�ã�S��PEF��S��cEF���������P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=ax+b��a��0����ͼ���뷴��������![]() ��k��0����ͼ����A����3��2����B��2��n����
��k��0����ͼ����A����3��2����B��2��n����
��1����������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����һ�κ���y=ax+b�Ľ���ʽ��
��3���۲�ͼ��ֱ��д������ʽax+b��![]() �Ľ⼯��
�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��д�����и�����![]() ����
����![]() �ĺ�����ϵʽ�����ж�
�ĺ�����ϵʽ�����ж�![]() �Ƿ�Ϊ
�Ƿ�Ϊ![]() ��һ�κ������Ƿ�Ϊ������������
��һ�κ������Ƿ�Ϊ������������
��1�������ε����Ϊ20�������εij�![]() ���
���![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2��������ʱ����ÿǧ��3.6Ԫ�������ϵ��ܼ�![]() Ԫ����������
Ԫ����������![]() ǧ��֮��ĺ�����ϵʽ��
ǧ��֮��ĺ�����ϵʽ��
��3���ֿ����з۱�400�У����ÿ���������36�У��ֿ������µķ۱ʺ���![]() ��������
��������![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��4���ְ�ΪС�ִ���һ�ݽ�������״δ���10 000Ԫ���Ժ�ÿ���´���500Ԫ����������![]() Ԫ������
Ԫ������![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����ֱ����ڱ�ʾ�����ڵļ����
12��![]() ��
��![]() ��
��![]() ��
��![]()
��1���������ϣ�{ }�� ��2���������ϣ�{ }��
��3���������ϣ�{ }�� ��4���������ϣ�{ }��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
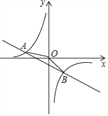
����Ŀ����ͼ����֪A����4��n����B��2����2����һ�κ���y=kx+b�ͷ���������y=![]() ��ͼ����������㣮
��ͼ����������㣮
��1����һ�κ����ͷ����������Ľ���ʽ��
��2��ֱ��д��ͼ����OAB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
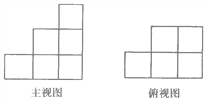
����Ŀ����һЩ��С��ͬ��С��������ɵļ����������ͼ����ͼ��ͼ29-29��ʾ.
(1)���㻭������������һ������ͼ.
(2)���������������С������Ŀ���Ϊn������д��n�����п���ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ,����
,����![]() .
.
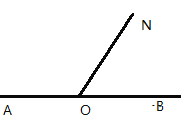
![]() �뻭��
�뻭��![]() ��ƽ����
��ƽ����![]() ;
;
![]() ���
���![]() ������
������![]() �ֱ��ʾ�ӵ�
�ֱ��ʾ�ӵ�![]() ��������������������ô����
����������������������![]() ��������
��������![]() ��ʾ ����.
��ʾ ����.
![]() ��
��![]() �������£���
�������£���![]() ʱ����ͼ���ҳ�������
ʱ����ͼ���ҳ�������![]() �����Ľǣ���Щ����_ .
�����Ľǣ���Щ����_ .
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com