练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知二次函数图象与x轴交于A，B两点，对称轴为直线x=2，下列结论：①abc>0； ②4a+b=0；③若点A坐标为(1，0)，则线段AB=5； ④若点M(x1，y1)、N(x2，y2)在该函数图象上，且满足0<x1<1，2<x2<3，则y1<y2其中正确结论的序号为（ ）

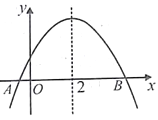
    A. ①，② B. ②，③ C. ③，④ D. ②，④

    【答案】D

    【解析】解：∵抛物线开口向下，∴a＜0．∵对称轴，∴b=－4a＞0．∵抛物线与y轴交点在y轴正半轴，∴c＞0，∴abc＜0，故①错误；

    由①得：b=－4a，∴4a+b=0，故②正确；

    若点A坐标为（1，0），因为对称轴为x=2，∴B（5，0），∴AB=5+1=6．故③错误；

    ∵a＜0，∴横坐标到对称轴的距离越大，函数值越小．∵0＜x1＜1，2＜x2＜3，∴ ，∴y1＜y2，故④正确．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读型综合题

    对于实数，我们定义一种新运算(其中，均为非零常数)，等式右边是通常的四则运算，由这种运算得到的数我们称之为线性数，记为，其中，叫做线性数的一个数对.若实数，都取正整数，我们称这样的线性数为正格线性数，这时的，叫做正格线性数的正格数对.

    (1)若，则_________，_________；

    (2)已知，.

    ①求字母的取值；

    ②若(其中为整数)，问是否有满足这样条件的正格数对？若有，请找出；若没有，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中,∠ACB=90°,经过点B的直线l(不与直线AB重合)与直线BC的夹角等于∠ABC,分别过点C、点A作直线l的垂线,垂足分别为点D、点E.

    (1)如图1,当点E与点B重合时,若AE=4,判断以C点为圆心CD长为半径的圆C与直线AB的位置关系并说明理由;

    (2)如图2,当点E在DB延长线上时,求证:AE=2CD;

    (3)记直线CE与直线AB相交于点F,若,,CD=4,求BD的长.

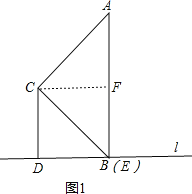
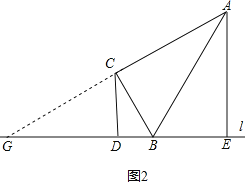
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB＝10，AC＝2，BC边上的高AD＝6，则另一边BC等于_______．

    【答案】10或6

    【解析】试题解析：根据题意画出图形，如图所示，

    如图1所示，AB=10，AC=2，AD=6，

    在Rt△ABD和Rt△ACD中，

    根据勾股定理得：BD==8，CD==2，

    此时BC=BD+CD=8+2=10；

    如图2所示，AB=10，AC=2，AD=6，

    在Rt△ABD和Rt△ACD中，

    根据勾股定理得：BD==8，CD==2，

    此时BC=BD-CD=8-2=6，

    则BC的长为6或10．

    【题型】填空题
    【结束】
    12

    【题目】在平面直角坐标系中，已知一次函数y=2x+1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＜x2，则y1 ______ y2．（填“＞”“＜”或“=”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】七年级开展演讲比赛，学校决定购买一些笔记本和钢笔作为奖品．现有甲、乙两家商店出售两种同样的笔记本和钢笔．他们的定价相同：笔记本定价为每本25元，钢笔每支定价6元，但是他们的优惠方案不同，甲店每买一本笔记本赠一支钢笔；乙店全部按定价的9折优惠．已知七年级需笔记本20本，钢笔x支（大于20支）．问：

    （1）在甲店购买需付款　 元，在乙店购买需付款　 元；

    （2）若x=30，通过计算说明此时到哪家商店购买较为合算？

    （3）当x=40时，请设计一种方案，使购买最省钱？算出此时需要付款多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线和直线外三点，按下列要求画图，填空：

    （1）画射线；

    （2）连接；

    （3）延长至，使得；

    （4）在直线上确定点，使得最小，请写出你作图的依据___________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，DE是⊙O的直径，过点D作⊙O的切线AD，C是AD的中点，AE交⊙O于点B，且四边形BCOE是平行四边形。

    (1)BC是⊙O的切线吗?若是，给出证明：若不是，请说明理由；

    (2)若⊙O半径为1，求AD的长。

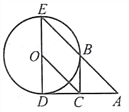
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把下列各数填入表示它所在的数集的大括号：

    ﹣2.4，3，21.08，0，﹣100，﹣（﹣2.28），，﹣|﹣4|，

    正有理数集合：{　 　}

    负有理数集合：{　 　}

    整数集合：{　 　}

    分数集合：{　 　}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

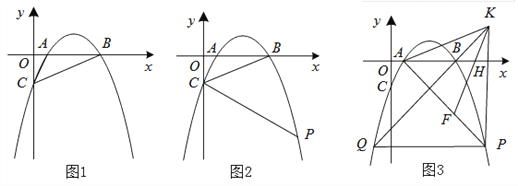
    【题目】在平面直角坐标系中，抛物线与x轴交于A、B（A点在B点的左侧）与y轴交于点C。

    （1）如图1，连接AC、BC，求△ABC的面积。

    （2）如图2：

    ①过点C作CR∥x轴交抛物线于点R，求点R的坐标；

    ②点P为第四象限抛物线上一点，连接PC，若∠BCP=2∠ABC时，求点P的坐标。

    （3）如图3，在（2）的条件下，点F在AP上，过点P作PH⊥x轴于H点，点K在PH的延长线上，AK=KF，∠KAH=∠FKH，PF=，连接KB并延长交抛物线于点Q，求PQ的长。

    查看答案和解析>>

    同步练习册答案