
【题目】在平面直角坐标系xOy中,直线y=kx+b(k≠0)与x轴交于点A,与y轴交于点B,与反比例函数y=![]() (m≠0)的图象在第一象限交于点P(1,3),连接OP.
(m≠0)的图象在第一象限交于点P(1,3),连接OP.
(1)求反比例函数y=![]() (m≠0)的表达式;
(m≠0)的表达式;
(2)若△AOB的面积是△POB的面积的2倍,求直线y=kx+b的表达式.
【答案】(1)y=![]() ;(2) y=﹣3x+6或y=x+2.
;(2) y=﹣3x+6或y=x+2.
【解析】分析:(1)把点P坐标代入反比例函数关系式y=![]() 即可求出m的值;
即可求出m的值;
(2)先根据△AOB的面积是△POB的面积的2倍求出点A的坐标,再用待定系数法求出一次函数解析式即可.
详解:(1)∵反比例函数y=![]() (m≠0)的图象经过点P(1,3),
(m≠0)的图象经过点P(1,3),
∴m=1×3=3,
∴反比例函数的表达式为y=![]() ;
;
(2)过P作PE⊥y轴于E,则PE=1.
∵△AOB的面积是△POB的面积的2倍,
∴![]() OBOA=
OBOA=![]() OBPE×2,
OBPE×2,
∴OA=2PE=2,
∴A(2,0)或A(﹣2,0).
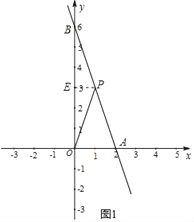
①当A点坐标为(2,0)时,如图1.
将A(2,0)、P(1,3)代入y=kx+b,
得![]() ,解得
,解得![]() ,
,
∴直线AB的表达式为y=﹣3x+6;
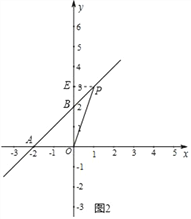
②当A点坐标为(﹣2,0)时,如图2.
将A(﹣2,0)、P(1,3)代入y=kx+b,
得![]() ,解得
,解得![]() ,
,
∴直线AB的表达式为y=x+2.
综上可知,直线AB的表达式为y=﹣3x+6或y=x+2.


科目:初中数学 来源: 题型:
【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
(1)如图1,△ABC是等腰锐角三角形,AB=AC(![]() ),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;
),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;
(2)如图2,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线;
(3)如图3,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数(如有需要,可在答题卡相应位置另外画图).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的统计图反映了我国2013年到2017年国内生产总值情况.(以上数据摘自国家统计局《中华人民共和国2017年国民经济和社会发展统计公报》)根据统计图提供的信息,下列推断不合理的是( )
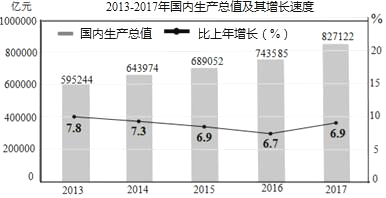
A. 与2016年相比,2017年我国国内生产总值有所增长
B. 2013﹣2016年,我国国内生产总值的增长率逐年降低
C. 2013﹣2017年,我国国内生产总值的平均增长率约为6.7%
D. 2016﹣2017年比2014﹣2015年我国国内生产总值增长的多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() (k≠0)的图象经过
(k≠0)的图象经过![]() ,
, ![]() 两点,二次函数
两点,二次函数![]() (其中a>2).
(其中a>2).

(1)求一次函数的表达式及二次函数图象的顶点坐标(用含a的代数式表示);
(2)利用函数图象解决下列问题:
①若![]() ,求当
,求当![]() 且
且![]() ≤0时,自变量x的取值范围;
≤0时,自变量x的取值范围;
②如果满足![]() 且
且![]() ≤0时的自变量x的取值范围内恰有一个整数,直接写出a的取值范围.
≤0时的自变量x的取值范围内恰有一个整数,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, OABC 的顶点 O、A、C 的坐标分别是(0,0),(2,0),(0.5,1),则点 B 的坐 标是( )
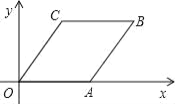
A.(1,2)B.(0.5,2)C.(2.5,1)D.(2,0.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】权威市调机构IDC发布了2018年第四季度全球智能手机出货量报告如下表:
手机品牌 | 2018年第四季度市场出货量(万台) | 2018年第四季度市场份额 | 2017年第四季度市场出货量(万台) | 2017年第四季度市场份额 |
Samsung | 70.4 | 18.7% | 74.5 | 18.9% |
Apple | 68.4 | 18.2% | 77.3 | 19.6% |
Huawei | 60.5 | 16.1% | 42.1 | 10.7% |
Xiaomi | 29.2 | 7.8% | 27.3 | 6.9% |
HMDGlobal | 28.6 | 7.6% | 28.2 | 7.1% |
Others | 118.4 | 31.5% | 145.3 | 36.8% |
总计 | 75.4 | 100.0% | 394.6 | 100.0% |
根据上表数据得出以下推断,其中结论正确的是( )
A.Huawei和Xiaomi2018年第四季度市场份额总和达到25%
B.2018年第四季度比2017年第四季度市场份额增幅最大的是Apple手机
C.Huawei手机2018年第四季度比2017年第四季度市场出货量增加18.4万合
D.2018年第四季度全球智能手机出货量同比下降约10%
查看答案和解析>>
科目:初中数学 来源: 题型:
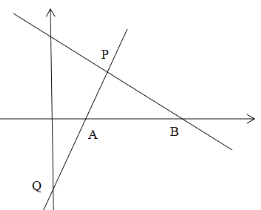
【题目】在平面直角坐标系中,直线y1=kx+b经过点P(2,2)和点Q(0,﹣2),与x轴交于点A,与直线y2=mx+n交于点P.
(1)求出直线y1=kx+b的解析式;
(2)当m<0时,直接写出y1<y2时自变量x的取值范围;
(3)直线y2=mx+n绕着点P任意旋转,与x轴交于点B,当△PAB是等腰三角形时,点B有几种位置?请你分别求出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线
与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
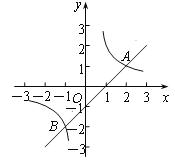
(1)求m及k的值;
(2)不解关于x、y的方程组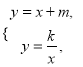 直接写出点B的坐标;
直接写出点B的坐标;
(3)直线![]() 经过点B吗?请说明理由.
经过点B吗?请说明理由.
【答案】(1)m=-1,k=2;(2)(-1,-2);(3)经过
【解析】试题分析:(1)把A(2,1)分别代入直线![]() 与双曲线
与双曲线![]() 即可求得结果;
即可求得结果;
(2)根据函数图象的特征写出两个图象的交点坐标即可;
(3)把x=-1,m=-1代入![]() 即可求得y的值,从而作出判断.
即可求得y的值,从而作出判断.
(1)把A(2,1)分别代入直线![]() 与双曲线
与双曲线![]() 的解析式得m=-1,k=2;
的解析式得m=-1,k=2;
(2)由题意得B的坐标(-1,-2);
(3)当x=-1,m=-1代入![]() 得y=-2×(-1)+4×(-1)=2-4=-2
得y=-2×(-1)+4×(-1)=2-4=-2
所以直线![]() 经过点B(-1,-2).
经过点B(-1,-2).
考点:反比例函数的性质
点评:反比例函数的性质是初中数学的重点,是中考常见题,一般难度不大,需熟练掌握.
【题型】解答题
【结束】
20
【题目】某气球内充满了一定质量的气球,当温度不变时,气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示(千帕是一种压强单位)
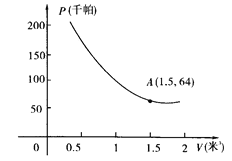
(1)写出这个函数的解析式;
(2)当气球的体积为0.8立方米时,气球内的气压是多少千帕;
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com