
分析 分别计算出[$\frac{2016}{1+(\frac{1}{30})^{4}}$]、[$\frac{2016}{1+(\frac{30}{1})^{4}}$]、[$\frac{2016}{1+(\frac{2}{29})^{4}}$]、[$\frac{2016}{1+(\frac{29}{2})^{4}}$]、[$\frac{2016}{1+(\frac{15}{16})^{4}}$]、[$\frac{2016}{1+(\frac{16}{15})^{4}}$]可知每两个数的和为2015,据此得出答案.
解答 解:∵[$\frac{2016}{1+(\frac{1}{30})^{4}}$]=[2016×$\frac{3{0}^{4}}{1+3{0}^{4}}$]=2015,[$\frac{2016}{1+(\frac{30}{1})^{4}}$]=[2016×$\frac{1}{1+3{0}^{4}}$]=0,
[$\frac{2016}{1+(\frac{2}{29})^{4}}$]=[2016×$\frac{2{9}^{4}}{16+2{9}^{4}}$]=2015,[$\frac{2016}{1+(\frac{29}{2})^{4}}$]=[2016×$\frac{16}{16+2{9}^{4}}$]=0,
[$\frac{2016}{1+(\frac{15}{16})^{4}}$]=[2016×$\frac{1{6}^{4}}{1{6}^{4}+1{5}^{4}}$]=1137,[$\frac{2016}{1+(\frac{16}{15})^{4}}$]=[2016×$\frac{1{5}^{4}}{1{5}^{4}+1{6}^{4}}$]=878,
∴原式=2015×15=30225,
故答案为:30225.
点评 本题主要考查有理数的混合运算及数字的变化规律,根据题意得出每两个数的和为2015是解题的关键.


科目:初中数学 来源: 题型:解答题
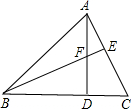 如图,AD是△ABC的边BC上的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD.
如图,AD是△ABC的边BC上的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | 第6列 | … | |
| 第1行 | -2 | 4 | -8 | a | -32 | 64 | … |
| 第2行 | 0 | 6 | -6 | 18 | -30 | 66 | … |
| 第3行 | -1 | 2 | -4 | 8 | -16 | b | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
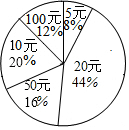 在一次救灾捐款活动中,某班50名同学人人拿出自己的零花线,有捐5元、10元、20元的,还有捐50元和100元的.如图所示的统计图反映了不同捐款数的人数比例,那么该班同学捐款的平均数、众数和中位数分别是31.2元、20元、20元.
在一次救灾捐款活动中,某班50名同学人人拿出自己的零花线,有捐5元、10元、20元的,还有捐50元和100元的.如图所示的统计图反映了不同捐款数的人数比例,那么该班同学捐款的平均数、众数和中位数分别是31.2元、20元、20元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com