
【题目】如图, DE AB 于 E , DF AC 于 F ,若 BD CD 、 BE CF ,
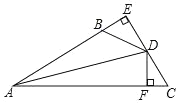
(1)求证:AD平分BAC ;
(2)已知AC 14,BE 2,求AB的长
【答案】(1)见解析;(2)10.
【解析】
(1)求出∠E=∠DFC=90°,根据全等三角形的判定定理得出Rt△BED≌Rt△CFD,推出DE=DF,根据角平分线性质得出即可;
(2)根据全等三角形的性质得出AE=AF,BE=CF,即可求出答案.
证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
∴在Rt△BED和Rt△CFD中,
![]() ,
,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC;
(2)解:∵Rt△BED≌Rt△CFD,
∴AE=AF,CF=BE=2,
∵AC=14,
∴AF=AC-CF=14-2=12.
在Rt△AED和Rt△AFD中,
∵![]() ,
,
∴Rt△AED≌Rt△AFD,
∴AE=AF=12,
∴AB=AE-BE=12-2=10.


科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级![]() 名学生进行测试,并把测试成绩(单位:
名学生进行测试,并把测试成绩(单位:![]() ) 绘制成不完整的频数分布表和频数分布直方图.
) 绘制成不完整的频数分布表和频数分布直方图.
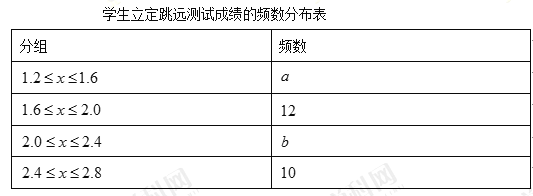

请根据图表中所提供的信息,完成下列问题
(1)表中![]() = ,
= ,![]() = ;
= ;
(2)请把频数分布直方图补充完整;
(3)跳远成绩大于等于![]() 为优秀,若该校九年级共有
为优秀,若该校九年级共有![]() 名学生,估计该年级学生立定跳远成绩优秀的学生有多少人?
名学生,估计该年级学生立定跳远成绩优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑车从邮局出发,先向南骑行2 km,到达A村,继续向南骑行3 km到达B村,然后向北骑行9 km到达C村,最后回到邮局.
(1)以邮局为原点,以向北为正方向,用0.5 cm表示1 km,画出数轴,并在该数轴上表示出A,B,C三个村庄的位置.
(2)C村离A村有多远?
(3)邮递员一共骑了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(原题)已知直线AB∥CD,点P为平行线AB,CD之间的一点.如图1,若∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,求∠BED的度数.
(探究)如图2,当点P在直线AB的上方时,若∠ABP=α,∠CDP=β,∠ABP和∠CDP的平分线交于点E1,∠ABE1与∠CDE1的角平分线交于点E2,∠ABE2与∠CDE2的角平分线交于点E3,…以此类推,求∠En的度数.
(变式)如图3,∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,试猜想∠P与∠E的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
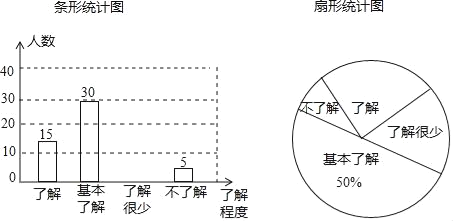
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计;
(3)若该中学共有学生1200人,估计该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都为1,在方格纸内将![]() 经过一次平移后得到
经过一次平移后得到![]() ,图中标出了点
,图中标出了点![]() 的对应点
的对应点![]() ,利用网格点和三角板画图或计算:
,利用网格点和三角板画图或计算:

(1)在给定方格纸中画出平移后的![]() .
.
(2)画出![]() 边的中线
边的中线![]() .
.
(3)画出![]() 边的高线
边的高线![]() .
.
(4)![]() 的面积为 .
的面积为 .
(5)在图中能使![]() 的格点
的格点![]() 的个数有 个 (点
的个数有 个 (点![]() 异于点
异于点![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度![]() (厘米)与燃烧时间
(厘米)与燃烧时间![]() (小时)之间的关系如图所示,其中乙蜡烛燃烧时
(小时)之间的关系如图所示,其中乙蜡烛燃烧时![]() 与
与![]() 之间的函数关系式是
之间的函数关系式是![]() .
.
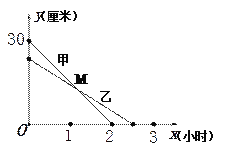
(1)甲蜡烛燃烧前的高度是_________厘米,乙蜡烛燃烧的时间是________小时.
(2)求甲蜡烛燃烧时![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)求出图中交点![]() 的坐标,并说明点
的坐标,并说明点![]() 的实际意义.
的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东西向的马路上有一个巡岗亭![]() ,巡岗员从岗亭
,巡岗员从岗亭![]() 出发以
出发以![]() 速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)第几次结束时巡逻员甲距离岗亭![]() 最远?距离
最远?距离![]() 有多远?
有多远?
(2)甲巡逻过程中配置无线对讲机,并一直与留守在岗亭![]() 的乙进行通话,问甲巡逻过程中,甲与乙保持通话的时长共多少小时?
的乙进行通话,问甲巡逻过程中,甲与乙保持通话的时长共多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com