
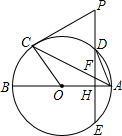
 如图,已知AB,AC分别是⊙O的直径和弦,D为劣弧AC上的一点,ED为⊙O的一条弦,交AB于点H,交AC于点F,过点C画⊙O的切线交ED的延长线于点P,且PC=PF.
如图,已知AB,AC分别是⊙O的直径和弦,D为劣弧AC上的一点,ED为⊙O的一条弦,交AB于点H,交AC于点F,过点C画⊙O的切线交ED的延长线于点P,且PC=PF.分析 (1)作辅助线,连接OC.根据切线的性质,OC⊥PC.根据PC=PF,OC=OA,可得:∠PCF=∠PFC,∠OCF=∠OAC.在Rt△FHA中,可得:∠FHA=90°,故AB⊥ED;
(2)连接AE,由点D是弧AC中点,得到∠DAF=∠DEA,推出△DAF∽△DEA,得到比例式,求得结果.
解答 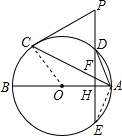 (1)证明:连接OC,
(1)证明:连接OC,
∵PC为⊙O的切线,
∴∠OCP=∠FCP+∠OCF=90°,
∵PC=PF,
∴∠PCF=∠PFC,
∵OA=OC,
∴∠OCA=∠OAC,
∵∠CFP=∠AFH,
∴∠AFH+∠OAC=90°,
∴∠AHF=90°,
即:AB⊥ED.
(2)连接AE.
∵点D是弧AC中点,
∴∠DAF=∠DEA,
∵∠ADE=∠ADE,
∴△DAF∽△DEA,
∴AD:ED=FD:AD,
∴AD2=DE•DF.
∴DE=$\frac{{AD}^{2}}{DF}$=$\frac{{4}^{2}}{3}$=$\frac{16}{3}$,
∴EF=DE-DF=$\frac{7}{3}$,
∵∠DAB=∠BED,
∴sin∠BED=sin∠DAB=$\frac{DH}{AD}$=$\frac{\frac{8}{3}}{4}$=$\frac{2}{3}$.
点评 本题考查了切线的判定已知此线过圆上某点,相似三角形的性质和判定,圆周角定理,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:选择题
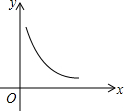 如图中的曲线是反比例函数y=$\frac{m+5}{x}$图象的一支,则m的取值范围是( )
如图中的曲线是反比例函数y=$\frac{m+5}{x}$图象的一支,则m的取值范围是( )| A. | m>-5 | B. | 0<m<5 | C. | -5<m<0 | D. | m<-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
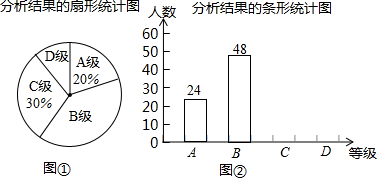
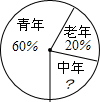 2015年1月份,某区体委组织“迎新春长跑活动”,现将报名的男选手分成:青年组、中年组、老年组,各组人数所占比例如图所示,已知青年组120人,则中年组的人数是40.
2015年1月份,某区体委组织“迎新春长跑活动”,现将报名的男选手分成:青年组、中年组、老年组,各组人数所占比例如图所示,已知青年组120人,则中年组的人数是40.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=2BD.则实数k的值为4$\sqrt{3}$.
如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=2BD.则实数k的值为4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 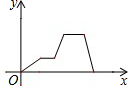 | B. | 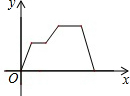 | C. | 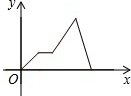 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
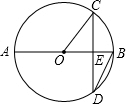 如图,AB是⊙O的直径,⊙O的半径$\sqrt{3}$cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )
如图,AB是⊙O的直径,⊙O的半径$\sqrt{3}$cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )| A. | $\frac{3}{2}$cm | B. | 3cm | C. | 2$\sqrt{3}$cm | D. | 9cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
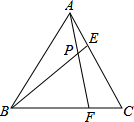 如图,等边三角形ABC的边长为6,点E、点F分别是AC、BC边上的点,连接AF,BE交于点P.给出以下判断:
如图,等边三角形ABC的边长为6,点E、点F分别是AC、BC边上的点,连接AF,BE交于点P.给出以下判断:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com