
【题目】如下图所示,![]() 两点在直线
两点在直线![]() 的两侧,在
的两侧,在![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离之差最大.
的距离之差最大.

科目:初中数学 来源: 题型:
【题目】已知,如图,在三角形![]() 中,
中,![]() ,
,![]() 于
于![]() ,且
,且![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时点
;同时点![]() 由
由![]() 点出发,沿
点出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,过点
,过点![]() 的动直线
的动直线![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,设运动时间为
,设运动时间为![]()
![]() ,解答下列问题:
,解答下列问题:

(1)线段![]() _________
_________![]() ;
;
(2)求证:![]() ;
;
(3)当![]() 为何值时,以
为何值时,以![]() 为顶点的四边形为平行四边形?
为顶点的四边形为平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,若∠DHO=20°,则∠ADC的度数是( )
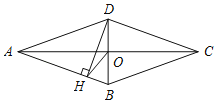
A. 120°B. 130°C. 140°D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店购进甲乙两种水果,销售过程中发现甲种水果比乙种水果销售量大,店主决定将乙种水果降价1元促销,降价后30元可购买乙种水果的斤数是原来购买乙种水果斤数的1.5倍.
(1)求降价后乙种水果的售价是多少元/斤?
(2)根据销售情况,水果店用不多于900元的资金再次购进两种水果共500斤,甲种水果进价为2元/斤,乙种水果进价为1.5元/斤,问至少购进乙种水果多少斤?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D 是边 BC 上的点(与 B、C 两点不重合),过点 D作 DE∥AC,DF∥AB,分别交 AB、AC 于 E、F 两点,下列说法正确的是( )

A. 若 AD 平分∠BAC,则四边形 AEDF 是菱形
B. 若 BD=CD,则四边形 AEDF 是菱形
C. 若 AD 垂直平分 BC,则四边形 AEDF 是矩形
D. 若 AD⊥BC,则四边形 AEDF 是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
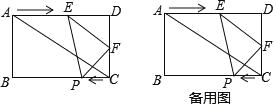
【题目】如图,在矩形 ABCD 中,AB=6cm,AD=8cm,直线 EF 从点 A 出发沿 AD 方向匀速运动,速度是 2cm/s,运动过程中始终保持 EF∥AC.F 交
AD 于 E,交 DC 于点 F;同时,点 P 从点 C 出发沿 CB 方向匀速运动,速度是 1cm/s,连接 PE、PF,设运动时间 t(s)(0<t<4).
(1)当 t=1 时,求 EF 长;
(2)求 t 为何值时,四边形 EPCD 为矩形;
(3)设△PEF 的面积为 S(cm2),求出面积 S 关于时间 t 的表达式;
(4)在运动过程中,是否存在某一时刻使 S△PC F:S 矩形 ABCD=3:16?若存在, 求出 t 的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
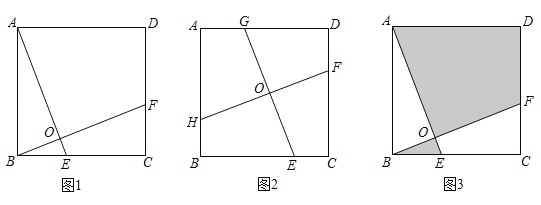
【题目】 在正方形ABCD中.
(1)如图1,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,试判断AE与BF的数量关系,并说明理由;
(2)如图2,点E、F、G、H分别在边BC、CD、DA、AB上,EG、FH相交于点O,∠GOH=90°,且EG=7,求FH的长;
(3)如图3,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,若AB=5,图中阴影部分的面积与正方形的面积之比为4:5,求△ABO的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分7分)已知关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com