
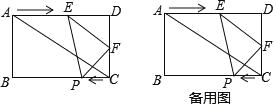
【题目】如图,在矩形 ABCD 中,AB=6cm,AD=8cm,直线 EF 从点 A 出发沿 AD 方向匀速运动,速度是 2cm/s,运动过程中始终保持 EF∥AC.F 交
AD 于 E,交 DC 于点 F;同时,点 P 从点 C 出发沿 CB 方向匀速运动,速度是 1cm/s,连接 PE、PF,设运动时间 t(s)(0<t<4).
(1)当 t=1 时,求 EF 长;
(2)求 t 为何值时,四边形 EPCD 为矩形;
(3)设△PEF 的面积为 S(cm2),求出面积 S 关于时间 t 的表达式;
(4)在运动过程中,是否存在某一时刻使 S△PC F:S 矩形 ABCD=3:16?若存在, 求出 t 的值;若不存在,请说明理由.
【答案】(1)EF=![]() ;(2)当 t=
;(2)当 t=![]() 时,四边形 EPCD 为矩形;(3)S=﹣
时,四边形 EPCD 为矩形;(3)S=﹣![]() t2+9t(0<t<4);(4)存在,当 t=2
t2+9t(0<t<4);(4)存在,当 t=2![]() 时,S△PCF:S 矩形 ABCD=3:16.
时,S△PCF:S 矩形 ABCD=3:16.
【解析】
(1)由勾股定理知AC=10,由题意得AE=2,DE=6,根据EF∥AC知△DEF∽△DAC,据此得![]() 代入计算;
代入计算;
(2)由DE∥CP且∠D=∠C知DE=CP时,四边形EPCD为矩形,据此求解
(3)证△DEF∽△DAC得![]() ,据此求得
,据此求得![]() ,
,![]() 根据S=S梯形DEPC-S△DEF-S△PCF可得函数解析式;
根据S=S梯形DEPC-S△DEF-S△PCF可得函数解析式;
(4)由S矩形ABCD=AB×AD=48,且S△PCF:S矩形ABCD=3:16知S△PCF=9,再根据![]() 可得关于t的方程,解之可得.
可得关于t的方程,解之可得.
解:(1)∵AB=6cm,AD=8cm,
∴AC=10cm,
当 t=1 时,AE=2, 则 DE=6,
∵EF∥AC,
∴△DEF∽△DAC,
∴![]() ,即
,即![]()
解得:![]()
(2)由题意知 AE=2t,CP=t, 则 DE=8﹣2t,
∵四边形 EPCD 是矩形,
∴DE=CP,即 8﹣2t=t, 解得 t= ![]() ,
,
故当 t=![]() 时,四边形 EPCD 为矩形;
时,四边形 EPCD 为矩形;
(3)∵EF∥AC,
∴△DEF∽△DAC,
![]() ,即
,即![]()
解得:![]()
则 CF=CDDF=6﹣(6﹣![]() t)=
t)=![]() t,
t,
则 S=S 梯形 DEPC﹣S△DEF﹣S△PCF
=![]() ×(8﹣2t+t)×6﹣
×(8﹣2t+t)×6﹣ ![]() ×(8﹣2t)×(6﹣
×(8﹣2t)×(6﹣![]() t)﹣
t)﹣![]() ×t×
×t×![]() t
t
=﹣![]() t2+9t,
t2+9t,
即 S=﹣![]() t2+9t(0<t<4);
t2+9t(0<t<4);
(4)存在,
∵S 矩形 ABCD=AB×AD=48,且 S△PCF:S 矩形 ABCD=3:16,
∴S△PCF=9,
又∵S△PCF=![]() ×t×
×t×![]() t=
t=![]() t2,
t2,
∴![]() t2=9,
t2=9,
解得:t=2![]() 或 t=﹣2
或 t=﹣2![]() (舍),
(舍),
∴当 t=2![]() 时,S△PCF:S 矩形 ABCD=3:16.
时,S△PCF:S 矩形 ABCD=3:16.


科目:初中数学 来源: 题型:
【题目】如图一次函数![]() 的图象分别交x轴、y轴于点A,B,与反比例函数
的图象分别交x轴、y轴于点A,B,与反比例函数![]() 图象在第二象限交于点C(m,6),
图象在第二象限交于点C(m,6),![]() 轴于点D,OA=OD.
轴于点D,OA=OD.
(1)求m的值和一次函数的表达式;
(2)在X轴上求点P,使△CAP为等腰三角形(求出所有符合条件的点)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子总结惨痛教训后.决定和乌龟再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(![]() 表示乌龟从起点出发所行的时间,
表示乌龟从起点出发所行的时间,![]() 表示乌龟所行的路程,
表示乌龟所行的路程,![]() 表示兔子所行的路程.下列说法中:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处上了乌龟.正确的有:( )
表示兔子所行的路程.下列说法中:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处上了乌龟.正确的有:( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
(1)若CE=8,CF=6,求OC的长;
(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
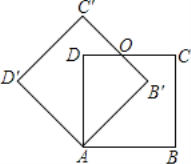
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转![]() 后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的面积是_________.
后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的面积是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 种商品以每件30元出售,
种商品以每件30元出售,![]() 种商品以每件100元出售.为满足市场需求,需购进
种商品以每件100元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共1000件,且
两种商品共1000件,且![]() 种商品的数量不少于
种商品的数量不少于![]() 种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
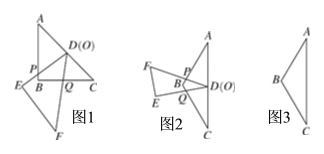
【题目】如图1,把两块全等的含45°角的直角三角板ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合.把三角板ABC固定不动,让三角板DEF绕点D旋转,两边分别与线段AB,BC相交于点P,Q,易说明△APD∽△CDQ.根据以上内容,回答下列问题:
(1)如图2,将含30°角的三角板DEF(其中∠EDF=30°)的锐角顶点D与等腰△ABC(其中∠ABC=120°)的底边中点O重合,两边DF,DE分别与边AB,BC相交于点P,Q.写出图中的相似三角形__ _ (直接填在横线上);
(2)其他条件不变,将三角板DEF旋转至两边DF,DE分别与边AB的延长线、边BC相交于点P,Q.上述结论还成立吗?请你在图3上补全图形,并说明理由;
(3)在(2)的条件下,连接PQ,△APD与△DPQ是否相似?请说明理由;
(4)根据(1)(2)的解答过程,你能否将两三角板改为更一般的三角形,使得(1)中的结论仍然成立?若能,请说明两个三角形应满足的条件;若不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com