
����Ŀ����ͼ1��������ȫ�ȵĺ�45���ǵ�ֱ�����ǰ�ABC��DEF������һ��ʹ���ǰ�DEF����Ƕ���D�����ǰ�ABC��б���е�O�غϣ������ǰ�ABC�̶������������ǰ�DEF�Ƶ�D��ת�����߷ֱ����߶�AB��BC�ཻ�ڵ�P��Q����˵����APD�ס�CDQ.�����������ݣ��ش��������⣺
(1)��ͼ2������30���ǵ����ǰ�DEF(������EDF��30��)����Ƕ���D�������ABC(������ABC��120��)�ĵױ��е�O�غϣ�����DF��DE�ֱ����AB��BC�ཻ�ڵ�P��Q.д��ͼ�е�����������__ _ (ֱ�����ں�����)��
(2)�����������䣬�����ǰ�DEF��ת������DF��DE�ֱ����AB���ӳ��ߡ���BC�ཻ�ڵ�P��Q.�������ۻ�������������ͼ3�ϲ�ȫͼ�Σ���˵�����ɣ�
(3)��(2)�������£�����PQ����APD����DPQ�Ƿ����ƣ���˵�����ɣ�
(4)����(1)(2)�Ľ����̣����ܷ������ǰ��Ϊ��һ��������Σ�ʹ��(1)�еĽ�����Ȼ���������ܣ���˵������������Ӧ����������������ܣ����Ҫ˵�����ɣ�
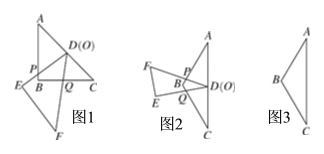
���𰸡�(1)��APD�ס�CDQ�� (2)������ͼ�����������ɼ�������(3)��APD�ס�DPQ�����ɼ�������(4)��DEF������EDF��������ABC ���㶥��Ϊ(180�㣭2��)�ĵ��������μ��������ɼ�����.
��������
��1��ͨ���ǵ�ת���ó���APD=��CDQ�������ɵó���APD�ס�CQD��
��2������֪�ɵ���BAC����BCA���ٸ�����֪���Ƶ��ó���APD����CDQ���̶��ɵó���APD�ס�CQD��
��3����APD�ס�DPQ���������£�����APD�ס�CDQ���ɵ�![]() ���ٸ��ݵ�DΪAC���е㣬�̶��ɵó�
���ٸ��ݵ�DΪAC���е㣬�̶��ɵó�![]() ���ٸ�����PAD����PDQ��30�㣬����֤����APD�ס�DPQ��
���ٸ�����PAD����PDQ��30�㣬����֤����APD�ס�DPQ��
��4����DEF������EDF��������ABC ���㶥��Ϊ(180�㣭2��)�ĵ��������μ���.
(1)�ߡ�ABC=120�㣬
���A=��C=30�㣬
�ߡ�ADP+��APD=150�㣬��ADP+��QDC=150�㣬
���APD=��CDQ��
���APD�ס�CDQ��
�ʴ�Ϊ����APD�ס�CDQ��
(2)��������ͼ���������£�
��AB��BC��
���BAC����BCA��
�ߡ�ABC��120�㣬
���BAC����BCA��30�㣬
���ADP����APD��180�㣭30�㣽150�㣬
�ߡ�EDF��30�㣬
���ADP����CDQ��150�㣬
���APD����CDQ��
���APD�ס�CDQ��
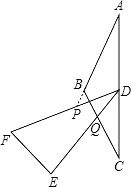
(3)��APD�ס�DPQ���������£�
��ͼ���ߡ�APD�ס�CDQ��
��![]() ��
��
����DΪAC���е㣬
��CD��AD��
��![]() ����
����![]() ��
��
���ߡ�PAD����PDQ��30�㣬
���APD�ס�DPQ��
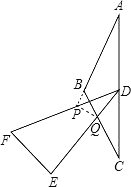
(4)��DEF������EDF��������ABC ���㶥��Ϊ(180�㣭2��)�ĵ��������μ�����
���ɣ��ߡ�ABC��180�㣭2����
���A����C������
�ߡ�ADP����APD��180�㣭������ADP����QDC��180�㣭����
���APD����CDQ��
���ߡ�A����C��
���APD�ס�CDQ.


 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳���![]() ������
������![]() ���ڵ�O�����ֱ����
���ڵ�O�����ֱ����![]() ���ڵ�
���ڵ�![]() ������AE�����н��ۣ�
������AE�����н��ۣ� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��![]() ʱ��
ʱ�� ![]() ��������ȷ���۵ĸ�����
��������ȷ���۵ĸ�����![]()

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
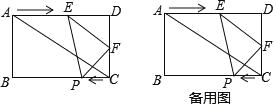
����Ŀ����ͼ���ھ��� ABCD �У�AB��6cm��AD��8cm��ֱ�� EF �ӵ� A ������ AD ���������˶����ٶ��� 2cm/s���˶�������ʼ�ձ��� EF��AC��F ��
AD �� E���� DC �ڵ� F��ͬʱ���� P �ӵ� C ������ CB ���������˶����ٶ��� 1cm/s������ PE��PF�����˶�ʱ�� t��s����0��t��4����
��1���� t��1 ʱ���� EF ����
��2���� t Ϊ��ֵʱ���ı��� EPCD Ϊ���Σ�
��3������PEF �����Ϊ S��cm2���������� S ����ʱ�� t �ı���ʽ��
��4�����˶������У��Ƿ����ijһʱ��ʹ S��PC F��S ���� ABCD��3��16�������ڣ� ��� t ��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ijУΪ���˽�ѧ���İ�ȫ��ʶ����ȫУ��Χ�������ȡ����ѧ�������ʾ����飮���ݵ���������ѧ���İ�ȫ��ʶ�ֳɡ�����������һ�㡱������ǿ��������ǿ���ĸ���Σ������Ƴ����������в�������ͳ��ͼ����ͼ��ʾ��
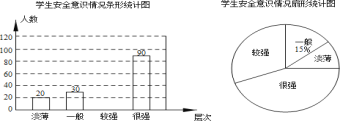
����������Ϣ������������⣺
��1����ε���һ����ȡ��______��ѧ����������ͳ��ͼ����������
��2������ͳ��ͼ�У�����ǿ�������ռԲ�ĽǵĴ�СΪ______�㣻
��3������У��3200��ѧ������Ҫ��ȫ��ʶΪ������������һ�㡱��ѧ��ǿ����ȫ���������ݵ��������������ȫУ��Ҫǿ����ȫ������ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��������ABCD�У�
��1����ͼ1����E��F�ֱ���BC��CD�ϣ�AE��BF�ཻ�ڵ�O����AOB=90�㣬���ж�AE��BF��������ϵ����˵�����ɣ�
��2����ͼ2����E��F��G��H�ֱ��ڱ�BC��CD��DA��AB�ϣ�EG��FH�ཻ�ڵ�O����GOH=90�㣬��EG=7����FH�ij���
��3����ͼ3����E��F�ֱ���BC��CD�ϣ�AE��BF�ཻ�ڵ�O����AOB=90�㣬��AB=5��ͼ����Ӱ���ֵ�����������ε����֮��Ϊ4��5�����ABO���ܳ���
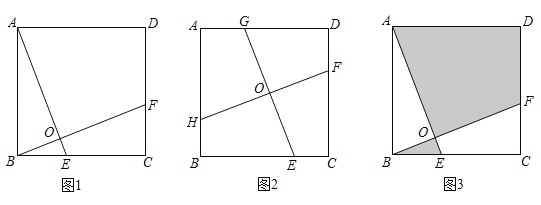
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ٰ�İ��꼶ѧ����ѧ������������![]() ����Ŀ:���ɰ�ƴͼ��Ȥ���ɽ⣬��ѧӦ�ã�ÿ����Ŀ�÷ֶ���һ���ٷֱ����������ܷ֣��ָܷߵĻ�ʤ���±�ΪС��С����λͬѧ�ĵ÷��������λ:�֣�:
����Ŀ:���ɰ�ƴͼ��Ȥ���ɽ⣬��ѧӦ�ã�ÿ����Ŀ�÷ֶ���һ���ٷֱ����������ܷ֣��ָܷߵĻ�ʤ���±�ΪС��С����λͬѧ�ĵ÷��������λ:�֣�:
���ɰ�ƴͼ | Ȥ���ɽ� | ��ѧӦ�� | |
�� |
|
|
|
�� |
|
|
|
![]() �����ɰ�ƴͼ��Ȥ���ɽ⣬��ѧӦ������÷ֱַ�
�����ɰ�ƴͼ��Ȥ���ɽ⣬��ѧӦ������÷ֱַ�![]() ����������ܷ֣�����˭�ܻ�ʤ?
����������ܷ֣�����˭�ܻ�ʤ?
![]() �����ɰ�ƴͼ��
�����ɰ�ƴͼ��![]() ���㣬С�� ������ܡ������ܡ�����ʤ��
���㣬С�� ������ܡ������ܡ�����ʤ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �� ��
�� ��![]() �ֱ����߶�
�ֱ����߶�![]() �ϣ���
�ϣ���![]()
![]() ��֤:
��֤:![]()
![]() ��֪
��֪![]() �ֱ���
�ֱ���![]() ���е㣬����
���е㣬����![]()
����![]() ����
����![]() �Ķ���:
�Ķ���:
������![]() ��
��![]() �ij�Ϊ��ֵʱ���ı���
�ij�Ϊ��ֵʱ���ı���![]() �Ǿ���?
�Ǿ���?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B��90����AC��12����A��60������D�ӵ�C������CA������ÿ��2����λ�����ٶ���A�������˶���ͬʱ��E�ӵ�A������AB������ÿ��1����λ�����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루t��0��������D��DF��BC�ڵ�F������DE��EF��
��1��AB�ij����� ����
��2����D��E���˶������У��߶�EF��AD�Ĺ�ϵ�Ƿ����仯�������仯����ô�߶�EF��AD�Ǻι�ϵ��������֤�������仯����˵�����ɣ�
��3���ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ�˵�����ɣ�
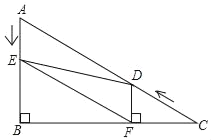
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ��� y��ax2+bx+c��a��0��������1��y1����2��y2����
���� y1��0 ʱ���� a+b+c��0
���� a��b ʱ���� y1��y2
���� y1��0��y2��0���� a+b��0���� a��0
���� b��2a��1��c��a��3���� y1��0���������ߵĶ���һ���ڵ������������ĸ��ж���ȷ���У� ������
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com