
【题目】某校举办的八年级学生数学素养大赛共设![]() 个项目:七巧板拼图,趣题巧解,数学应用,每个项目得分都按一定百分比折算后计入总分,总分高的获胜,下表为小米和小麦两位同学的得分情况(单位:分):
个项目:七巧板拼图,趣题巧解,数学应用,每个项目得分都按一定百分比折算后计入总分,总分高的获胜,下表为小米和小麦两位同学的得分情况(单位:分):
七巧板拼图 | 趣题巧解 | 数学应用 | |
小米 |
|
|
|
小麦 |
|
|
|
![]() 若七巧板拼图,趣题巧解,数学应用三项得分分别
若七巧板拼图,趣题巧解,数学应用三项得分分别![]() 按折算计入总分,最终谁能获胜?
按折算计入总分,最终谁能获胜?
![]() 若七巧板拼图按
若七巧板拼图按![]() 折算,小麦 (填“可能”或“不可能”)获胜.
折算,小麦 (填“可能”或“不可能”)获胜.
科目:初中数学 来源: 题型:
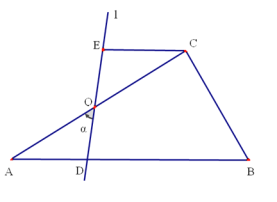
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点O是
.点O是![]() 的中点,过点O的直线
的中点,过点O的直线![]() 与从
与从![]() 重合的位置开始,绕点O作逆时针旋转,交
重合的位置开始,绕点O作逆时针旋转,交![]() 于点D,过点C作
于点D,过点C作![]() 交直线
交直线![]() 于点E,设直线
于点E,设直线![]() 的旋转角为
的旋转角为![]() .
.
(1)当四边形![]() 是等腰梯形时,则
是等腰梯形时,则![]() =_______,此时
=_______,此时![]() ________;
________;
(2)当四边形![]() 是直角梯形时,则
是直角梯形时,则![]() =_________,此时
=_________,此时![]() _________;
_________;
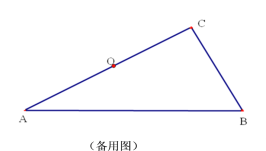
(3)当![]() 为几度时,判断四边形
为几度时,判断四边形![]() 是否为菱形,并说明理由.
是否为菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
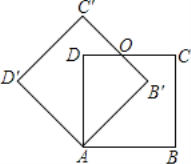
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转![]() 后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的面积是_________.
后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的面积是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
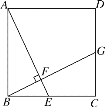
【题目】如图,在正方形ABCD中,点E在边BC上(点E不与点B重合),连接AE,过点B作BF⊥AE于点F,交CD于点G.
(1)求证:△ABF∽△BGC;
(2)若AB=2,G是CD的中点,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
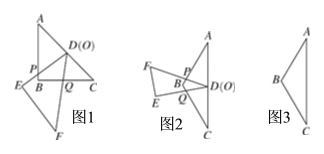
【题目】如图1,把两块全等的含45°角的直角三角板ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合.把三角板ABC固定不动,让三角板DEF绕点D旋转,两边分别与线段AB,BC相交于点P,Q,易说明△APD∽△CDQ.根据以上内容,回答下列问题:
(1)如图2,将含30°角的三角板DEF(其中∠EDF=30°)的锐角顶点D与等腰△ABC(其中∠ABC=120°)的底边中点O重合,两边DF,DE分别与边AB,BC相交于点P,Q.写出图中的相似三角形__ _ (直接填在横线上);
(2)其他条件不变,将三角板DEF旋转至两边DF,DE分别与边AB的延长线、边BC相交于点P,Q.上述结论还成立吗?请你在图3上补全图形,并说明理由;
(3)在(2)的条件下,连接PQ,△APD与△DPQ是否相似?请说明理由;
(4)根据(1)(2)的解答过程,你能否将两三角板改为更一般的三角形,使得(1)中的结论仍然成立?若能,请说明两个三角形应满足的条件;若不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,![]() cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年1月1日新交通法规开始实施.为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A:从不闯红灯;B:偶尔闯红灯;C:经常闯红灯;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,解答下列问题:
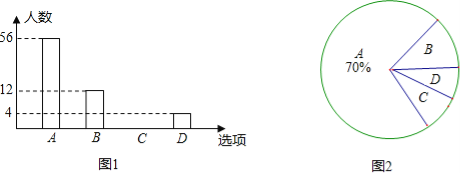
(1)本次调查共选取 名居民;
(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(3)如果该社区共有居民1600人,估计有多少人从不闯红灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
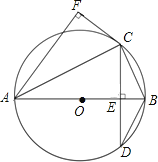
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
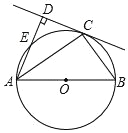
【题目】如图,AB 为⊙O 的直径,点 C 为⊙O 上一点,AD 和过点 C 的切线相互垂直,垂足为 D.
(1)求证:AC 平分∠DAB;
(2)AD 交⊙O 于点 E,若 AD=3CD=9,求 AE 的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com