
【题目】2013年1月1日新交通法规开始实施.为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A:从不闯红灯;B:偶尔闯红灯;C:经常闯红灯;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,解答下列问题:
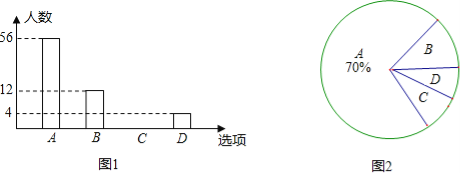
(1)本次调查共选取 名居民;
(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(3)如果该社区共有居民1600人,估计有多少人从不闯红灯?
科目:初中数学 来源: 题型:
【题目】特殊两位数乘法的速算——如果两个两位数的十位数字相同,个位数字相加为10,那么能立说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C,B+C=10,A>3),那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.
如:47×43=2021,61×69=4209.
(1)请你直接写出83×87的值;
(2)设这两个两位数的十位数字为x(x>3),个位数字分别为y和z(y+z=10),通过计算验证这两个两位数的乘积为100x(x+1)+yz.
(3)99991×99999=___________________(直接填结果)
【答案】7221
【解析】分析:![]() 套用上面的归纳总结代入数据,即可得出结论;
套用上面的归纳总结代入数据,即可得出结论;
![]() 利用上面总结的结论套入数据表示出该两个两位数的成绩,在将等式展开合并同类项得出左边=右边,从而证明结论成立.
利用上面总结的结论套入数据表示出该两个两位数的成绩,在将等式展开合并同类项得出左边=右边,从而证明结论成立.
![]() 直接运算即可.
直接运算即可.
详解:(1)83和87满足题中的条件,即十位数都是8,8>3,且个位数字分别是3和7,之和为10,那么它们的乘积是一个4位数,前两位数字是8和9的乘积,后两位数字就是3和7的乘积,因而,答案为:7221.
(2) 这两个两位数的十位数字为x(x>3),个位数字分别为y和z,则由题知y+z=10,
因而有:(10x+y)(10x+z)=100x2+10xz+10xy+yz
=100x2+10x(y+z)+yz,
=100x2+100x+yz,
=100x(x+1)+yz.
(3)9999000009.
点睛:通过阅读题干掌握题中所给信息得出推理方法,然后通过多项式的展开式得出答案.学生应熟练掌握归纳推理的数学思想.
【题型】解答题
【结束】
19
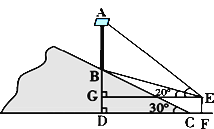
【题目】为了大力弘扬和践行社会主义核心价值观,某乡镇在一条公路旁的小山坡上,树立一块大型标语牌AB,如图所示,标语牌底部B点到山脚C点的距离BC为20米,山坡的坡角为30°. 某同学在山脚的平地F处测量该标语牌的高,测得点C到测角仪EF的水平距离CF = 1.7米,同时测得标语牌顶部A点的仰角为45°,底部B点的仰角为20°,求标语牌AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 为平面内一点.
为平面内一点.
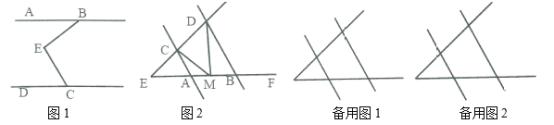
(1)如图1,![]() 和
和![]() 互余,小明说过
互余,小明说过![]() 作
作![]() ,很容易说明
,很容易说明![]() 。请帮小明写出具体过程;
。请帮小明写出具体过程;
(2)如图2,![]() ,当点
,当点![]() 在线段
在线段![]() 上移动时(点
上移动时(点![]() 与
与![]() ,
,![]() 两点不重合),指出
两点不重合),指出![]() 与
与![]() ,
,![]() 的数量关系?请说明理由;
的数量关系?请说明理由;
(3)在(2)的条件下,若点![]() 在
在![]() ,
,![]() 两点外侧运动(点
两点外侧运动(点![]() 与
与![]() ,
,![]() ,
,![]() 三点不重合)请直接写出
三点不重合)请直接写出![]() 与
与![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探索发现】
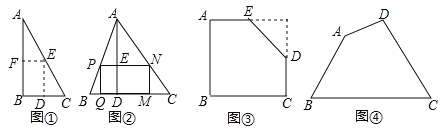
如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P的坐标是(a,b),从-2,-1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得
不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得![]() 成立的一对数m,n为“相伴数对”,记为(m,n).
成立的一对数m,n为“相伴数对”,记为(m,n).
(1)若(m,1)是“相伴数对”,则m=_____;
(2)(m,n)是“相伴数对”,则代数式![]() m﹣[n+
m﹣[n+![]() (6﹣12n﹣15m)]的值为_____.
(6﹣12n﹣15m)]的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:OB、OC、OE是∠AOD内的射线,若∠AOD=130°.
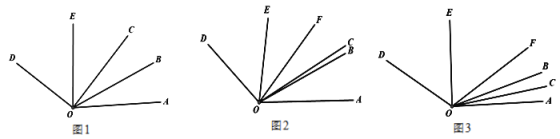
(1)如图1,OB是∠AOC的平分线,OE是∠COD的平分线,∠BOE=_____度;
(2)OF也是∠AOD内的射线,如图2,若∠FOC=20°,OB平分∠AOF,OE平分∠COD,当射线OC绕点O在∠AOF内旋转时,求∠BOE的大小;
(3)在(2)的条件下,当射线OC从边OA开始绕O点以每秒2°的速度逆时针旋转t秒,如图3,若∠AOB:∠DOE=2:3,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com