练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一般情况下不成立，但有些数可以使得它成立，例如：m=n=0时，我们称使得成立的一对数m，n为“相伴数对”，记为（m，n）．

    （1）若（m，1）是“相伴数对”，则m=_____；

    （2）（m，n）是“相伴数对”，则代数式m﹣[n+（6﹣12n﹣15m）]的值为_____．

    【答案】﹣﹣3

    【解析】

    （1）利用新定义“相伴数对”列出算式，计算即可求出m的值；（2）利用新定义“相伴数对”列出关系式，原式去括号合并后代入计算即可求出值．

    (1)根据题意得：，

    去分母得：15m+10=6m+6，

    移项合并得：9m=4，

    解得：m=；

    (2)由题意得：,即，

    整理得：15m+10n=6m+6n，即9m+4n=0，

    则原式=mn3+6n+m=m+5n3= (9m+4n)3=3，

    故答案为：(1) ;(2)3

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了贯彻教育部关于中小学生“每天锻炼一小时”的要求，某市教育局做了一次随机抽样调查，其内容是：（1）学生每天锻炼时间是否达到1小时；（2）学生每天锻炼时间未达到1小时的原因．随机调查了600名学生，把所得的数据制成了如下的扇形统计图和条形统计图（不完整）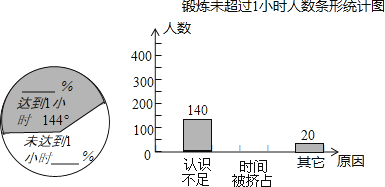
    根据图示，回答以下问题：
    （1）每天锻炼时间达到1小时的人数占被调查总人数的百分比是；
    每天锻炼时间未达到1小时的人数占被调查总人数的百分比是；
    每天锻炼时间未达到1小时的人数为人，其中原因是“时间被挤占”的人数是人；
    （2）补全扇形统计图和条形统计图；
    （3）若该市现有中小学生约27万人，据此调查，可估计今年该市中小学生每天锻炼未达到1小时的学生约有多少万人？
    （4）从这次接受调查的学生中，随机抽取一名学生的“每天锻炼一小时”的情况，回答内容为“时间被挤占”的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某小型企业实行工资与业绩挂钩制度，工人工资分为A、B、C、D四个档次．小明对该企业三月份工人工资进行调查，并根据收集到的数据，绘制了如下尚不完整的统计表与扇形统计图．

    根据上面提供的信息，回答下列问题：
    （1）求该企业共有多少人？
    （2）请将统计表补充完整；
    （3）扇形统计图中“C档次”的扇形所对的圆心角是度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算与化简．

    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴上，两点对应的数分别为，，且满足；

    求，的值；

    若点以每秒个单位，点以每秒个单位的速度同时出发向右运动，多长时间后，两点相距个单位长度？

    已知从向右出发，速度为每秒一个单位长度，同时从向右出发，速度为每秒个单位长度，设的中点为，的值是否变化？若不变求其值；否则说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某车间有120名工人，为了了解这些工人日加工零件数的情况，随机抽出其中的30名工人进行调查．整理调查结果，绘制出不完整的条形统计图（如图）．根据图中的信息，解答下列问题：
    （1）在被调查的工人中，日加工9个零件的人数为名；
    （2）在被调查的工人中，日加工12个零件的人数为名，日加工个零件的人数最多，日加工15个零件的人数占被调查人数的%；
    （3）依据本次调查结果，估计该车间日人均加工零件数和日加工零件的总数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中， 为坐标原点，点在反比例函数的图象上，作轴于点．

    （1）的面积为______；

    （2）若点的横坐标为4，点在轴的正半轴，且是等腰三角形，求点的坐标；

    （3）动点从原点出发，沿轴的正方向运动，以为直角边，在的右侧作等腰， ；若在点运动过程中，斜边始终在轴上，求 的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】考试前，同学们总会采用各种方式缓解考试压力，以最佳状态迎接考试．某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动，学校将减压方式分为五类，同学们可根据自己的情况必选且只选其中一类．数据收集整理后，绘制了图1和图2两幅不完整的统计图，请根据统计图中的信息解答下列问题：

    （1）请通过计算，补全条形统计图；

    （2）请直接写出扇形统计图中“享受美食”所对应圆心角的度数为　　；

    （3）根据调查结果，可估计出该校九年级学生中减压方式的众数和中位数分别是　　，　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴与C、A两点，点B是x轴上一点，且横坐标为2，在OA上取一点H，使得OH=OB.

    （1） 求点C的坐标.

    （2） 求CH所在直线的表达式.

    （3） 若点P在直线CH上运动，是否存在一点P，使得△PBC的面积是△AHB面积的,若存在，求出点P的坐标，若不存在，说明理由.

    查看答案和解析>>

    同步练习册答案