
【题目】如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴与C、A两点,点B是x轴上一点,且横坐标为2,在OA上取一点H,使得OH=OB.
(1) 求点C的坐标.
(2) 求CH所在直线的表达式.
(3) 若点P在直线CH上运动,是否存在一点P,使得△PBC的面积是△AHB面积的![]() ,若存在,求出点P的坐标,若不存在,说明理由.
,若存在,求出点P的坐标,若不存在,说明理由.

【答案】(1)(-3,0)(2)y=![]() x+2(3)(-2,
x+2(3)(-2, ![]() )(-4,-
)(-4,-![]() )
)
【解析】分析:(1)令y=0,求出x的值,即可得到C点的坐标;
(2)先确定点B的坐标和H的坐标,即可求出直线CH的解析式;
(3)先求出△ABH的面积,进而得出△PBC的面积,利用面积公式求出点P的纵坐标,即可得出结论.
详解:(1)直线y=x+3,当y=0时,x=-3
![]() 点
点![]() 的坐标是(-3,0).
的坐标是(-3,0).
(2)∵OB=OH,B点横坐标为2
∴H(0,2)
设直线CH的表达式为y=kx+b
把C(-3,0),H(0,2)代入直线CH的表达式得k=![]() ,b=2
,b=2
∴直线CH的表达式为y=![]() x+2
x+2
(3)S△AHB=![]() AH·OH=
AH·OH=![]() ×2×1=1
×2×1=1
S△PBC=![]() S△AHB=
S△AHB=![]()
设P(m,n),
S△PBC=![]() ·BC·|n|=
·BC·|n|=![]() ×5·|n|=
×5·|n|=![]()
|n|=![]()
∴n=±![]()
∴P1(m, ![]() ),P2(m,-
),P2(m,-![]() )
)
将P1,P2代入直线CH的表达式y=![]() x+2 中得,
x+2 中得,
P1(-2, ![]() ),P2(-4,-
),P2(-4,-![]() )
)


科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得
不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得![]() 成立的一对数m,n为“相伴数对”,记为(m,n).
成立的一对数m,n为“相伴数对”,记为(m,n).
(1)若(m,1)是“相伴数对”,则m=_____;
(2)(m,n)是“相伴数对”,则代数式![]() m﹣[n+
m﹣[n+![]() (6﹣12n﹣15m)]的值为_____.
(6﹣12n﹣15m)]的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
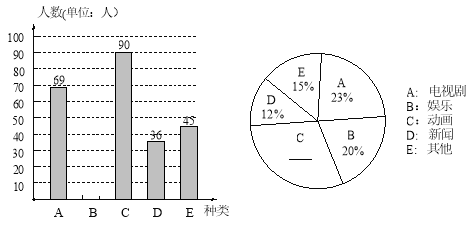
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有2000名学生,请估计该校喜爱电视剧节目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【证法回顾】证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.
求证: .
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;
请继续完成证明过程:

(2)【问题解决】
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)【拓展研究】
如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=![]() ,DF=2,∠GEF=90°,求GF的长.
,DF=2,∠GEF=90°,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)体育课上,某中学对七年级男生进行了引体向上测试,以能做7个为标准多于标准的次
数记为正数,不足的次数记为负数,其中8名男生的成绩为+2,-1,+3,0,-2,-3,+1,0.
(1)这8名男生中达到标准的占百分之几?
(2)他们共做了多少次引体向上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家经销一种绿茶,用于装修门面已投资3000元,已知绿茶每千克成本50元,在第一个月的试销时间内发现,销量w(kg)随销售单价x(元/kg)的变化而变化,具体变化规律如下表所示
销售单价x(元/kg) | … | 70 | 75 | 80 | 85 | 90 | … |
销售量w(kg) | … | 100 | 90 | 80 | 70 | 60 | … |
设该绿茶的月销售利润为y(元)(销售利润=单价×销售量﹣成本﹣投资).
(1)请根据上表,写出w与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求y与x之间的函数关系式(不必写出自变量x的取值范围).并求出x为何值时,y的值最大?
(3)若在第一个月里,按使y获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于90元,要想在全部收回投资的基础上使第二个月的利润达到1700元,那么第二个月里应该确定销售单价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=16 km,CB=11 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0;②当-1≤x≤3时,y<0;③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,
其中正确的是( )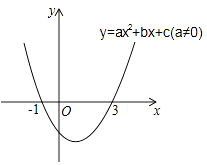
A.①②③
B.①②④
C.①④
D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com