
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0;②当-1≤x≤3时,y<0;③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,
其中正确的是( )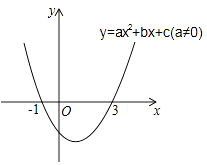
A.①②③
B.①②④
C.①④
D.②③④
【答案】C
【解析】解:①∵函数图象的对称轴为:x=- ![]() =
= ![]() =1
=1
∴b=-2a,即2a+b=0,故①正确;
②∵抛物线开口方向朝上,
∴a>0,
又∵二次函数y=ax2+bx+c的图象与x轴交点为(-1,0)、(3,0),
∴当-1≤x≤3时,y≤0,故②错误;
③∵抛物线的对称轴为x=1,开口方向向上,
∴若(x1 , y1)、(x2 , y2)在函数图象上,当1<x1<x2时,y1<y2;当x1<x2<1时,y1>y2;
故③错误;
④∵二次函数y=ax2+bx+c的图象过点(3,0),
∴x=3时,y=0,即9a+3b+c=0,故④正确.
故选:C.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴与C、A两点,点B是x轴上一点,且横坐标为2,在OA上取一点H,使得OH=OB.
(1) 求点C的坐标.
(2) 求CH所在直线的表达式.
(3) 若点P在直线CH上运动,是否存在一点P,使得△PBC的面积是△AHB面积的![]() ,若存在,求出点P的坐标,若不存在,说明理由.
,若存在,求出点P的坐标,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某河的两岸PQ、MN互相平行,河岸PQ上的点A处和点B处各有一棵大树,AB=30米,某人在河岸MN上选一点C,AC⊥MN,在直线MN上从点C前进一段路程到达点D,测得∠ADC=30°,∠BDC=60°,求这条河的宽度.( ![]() ≈1.732,结果保留三个有效数字).
≈1.732,结果保留三个有效数字).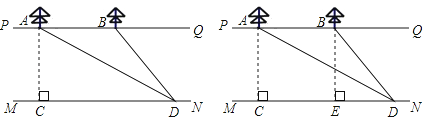
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若![]() ,AB=2,则图中阴影部分的面积为______.
,AB=2,则图中阴影部分的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(﹣1)2018﹣8÷(﹣2)3+4×(﹣![]() )3;
)3;
(2)先化简,再求值:3(a2b﹣2ab2)﹣(3a2b﹣2ab2),其中|a﹣1|+(b+![]() )2=0.
)2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1 , x2 .
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )

A、120° B、135° C、150° D、45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com