
【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若![]() ,AB=2,则图中阴影部分的面积为______.
,AB=2,则图中阴影部分的面积为______.

科目:初中数学 来源: 题型:
【题目】(1)【证法回顾】证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.
求证: .
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;
请继续完成证明过程:

(2)【问题解决】
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)【拓展研究】
如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=![]() ,DF=2,∠GEF=90°,求GF的长.
,DF=2,∠GEF=90°,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=16 km,CB=11 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
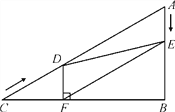
【题目】如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF。
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,AB=4,过圆心O的直线垂直AB于点D,交⊙O于点C和点E,连接AC、BC、OB,cos∠ACB= ![]() ,延长OE到点F,使EF=2OE.
,延长OE到点F,使EF=2OE. 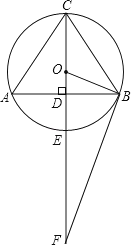
(1)求⊙O的半径;
(2)求证:BF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
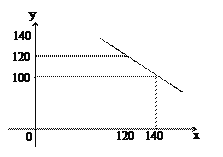
【题目】某商店试销一种成本单价为100元/件的运动服,规定试销时的销售单价不低于成本单价,又不高于180元/件,经市场调查,发现销售量y(件)与销售单价x(元)之间的关系满足一次函数y=kx+b(k≠0),其图象如图。
(1)根据图象,求一次函数的解析式;
(2)当销售单价x在什么范围内取值时,销售量y不低于80件。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0;②当-1≤x≤3时,y<0;③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,
其中正确的是( )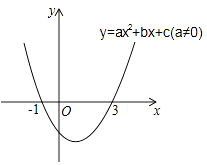
A.①②③
B.①②④
C.①④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
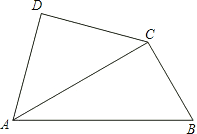
【题目】将一副三角尺如图拼接:含![]() 角的三角尺
角的三角尺![]() 的长直角边与含
的长直角边与含![]() 角的三角尺
角的三角尺![]() 的斜边恰好重合
的斜边恰好重合![]() 已知
已知![]() 是AC上的一个动点.
是AC上的一个动点.
![]() 当点P运动到
当点P运动到![]() 的平分线上时,连接DP,求DP的长;
的平分线上时,连接DP,求DP的长;
![]() 当点P在运动过程中出现
当点P在运动过程中出现![]() 时,求此时
时,求此时![]() 的度数;
的度数;
![]() 当点P运动到什么位置时,以
当点P运动到什么位置时,以![]() 为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.
为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
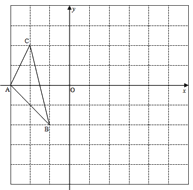
【题目】如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为:A(-3,0),B(-1,-2),C(-2,2).
(1)请在图中画出△ABC绕B点顺时针旋转90°后的图形△A′BC′.
(2)请直接写出以A′、B、C′为顶点平行四边形的第4个顶点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com