
【题目】如图,某河的两岸PQ、MN互相平行,河岸PQ上的点A处和点B处各有一棵大树,AB=30米,某人在河岸MN上选一点C,AC⊥MN,在直线MN上从点C前进一段路程到达点D,测得∠ADC=30°,∠BDC=60°,求这条河的宽度.( ![]() ≈1.732,结果保留三个有效数字).
≈1.732,结果保留三个有效数字).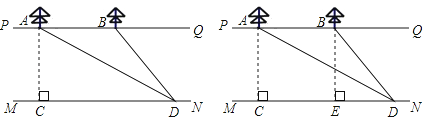
【答案】解:过点B作BE⊥MN于点E,则CE=AB=30米,CD=CE+ED,AC=BE,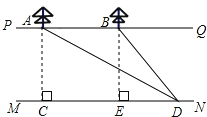
设河的宽度为x,
在Rt△ACD中,
∵AC⊥MN,CE=AB=30米,∠ADC=30°,
∴ ![]() =tan∠ADC,即
=tan∠ADC,即 ![]() ①,
①,
在Rt△BED中,![]() =tan∠BDC,
=tan∠BDC, ![]() =
= ![]() ②,
②,
①②联立得,x=15 ![]() ≈26.0(米).
≈26.0(米).
答:这条河的宽度为26.0米.
【解析】过点B作BE⊥MN于点E,则CE=AB=30米,CD=CE+ED,AC=BE,在Rt△ACD中,由锐角三角函数的定义可知, ![]() =tan∠ADC,在Rt△BED中,
=tan∠ADC,在Rt△BED中, ![]() =tan∠BDC,两式联立即可得出AC的值,即这条河的宽度.
=tan∠BDC,两式联立即可得出AC的值,即这条河的宽度.
【考点精析】通过灵活运用关于方向角问题,掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角即可以解答此题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
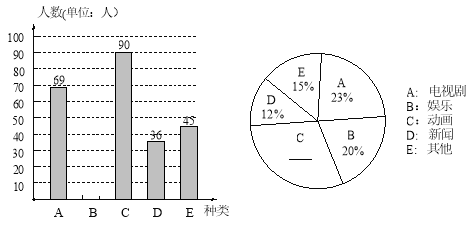
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有2000名学生,请估计该校喜爱电视剧节目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=16 km,CB=11 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
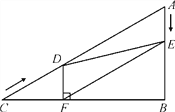
【题目】如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF。
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,AB=4,过圆心O的直线垂直AB于点D,交⊙O于点C和点E,连接AC、BC、OB,cos∠ACB= ![]() ,延长OE到点F,使EF=2OE.
,延长OE到点F,使EF=2OE. 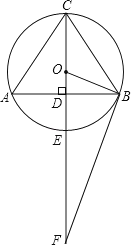
(1)求⊙O的半径;
(2)求证:BF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0;②当-1≤x≤3时,y<0;③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,
其中正确的是( )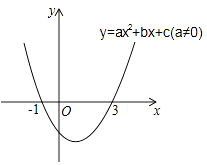
A.①②③
B.①②④
C.①④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张规格、质地相同的卡片,它们背面完全相同,正面图案分别是A.平行四边形,B.菱形,C.矩形,D.正方形,将这四张卡片背面朝上洗匀后.
(1)随机抽取一张卡片图案是轴对称图形的概率是;
(2)随机抽取两张卡片(不放回),求两张卡片卡片图案都是轴对称图形的概率,并用树状图或列表法加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com