
【题目】如图,在平面直角坐标系中, ![]() 为坐标原点,点
为坐标原点,点![]() 在反比例函数
在反比例函数![]() 的图象上,作
的图象上,作![]() 轴于
轴于![]() 点.
点.
(1)![]() 的面积为______;
的面积为______;
(2)若点![]() 的横坐标为4,点
的横坐标为4,点![]() 在
在![]() 轴的正半轴,且
轴的正半轴,且![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标;
的坐标;
(3)动点![]() 从原点出发,沿
从原点出发,沿![]() 轴的正方向运动,以
轴的正方向运动,以![]() 为直角边,在
为直角边,在![]() 的右侧作等腰
的右侧作等腰![]() ,
, ![]() ;若在点
;若在点![]() 运动过程中,斜边
运动过程中,斜边![]() 始终在
始终在![]() 轴上,求
轴上,求 ![]() 的值.
的值.



【答案】6
【解析】分析: (1)首先过点B作BC⊥x轴于点C,由等腰三角形的三线合一,可得OC=AC=3,然后由顶点B在反比例函数![]() 的图象上,求得点B的坐标;
的图象上,求得点B的坐标;
(2)首先由等腰直角三角形的性质,可得OC=BC,然后由顶点B在反比例函数![]() 的图象上,求得点B的坐标,继而求得点A的坐标;
的图象上,求得点B的坐标,继而求得点A的坐标;
(3)首先过点P作PD⊥x轴于点D,易得AD=PD,则可设AD=b,则点P(4![]() +b,b),又由点P在反比例函数
+b,b),又由点P在反比例函数![]() 的图象上,求得b的值,继而求得答案.
的图象上,求得b的值,继而求得答案.
详解:
(1) 6
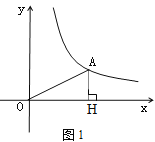
(2)依题意,得A(4,3),如图1,过A作AH⊥x轴于H,
∴AH=3,OH=4, ![]() ;
;
要使△OAP是等腰三角形,有如下三种情况:
①当OP=OA时,OP=5
∴点P的坐标为(5,0)
②当AO=AP时,OP=2OH=8
∴点P的坐标为(8,0)
③当PO=PA时,如图2,设点P的横坐标为![]() ,
,
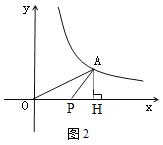
则PO=PA= ![]() ,PH=
,PH=![]()
在Rt△AHP中, ![]()
∴![]()
解得: ![]()
∴点P的坐标为(![]() ,0)
,0)
综上所述,点P的坐标为(5,0)或 (8,0) 或(![]() ,0)
,0)
(3)如图3,
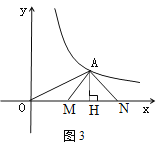
在等腰Rt△MAN,
∵AH⊥x轴于H
∴MH=AH=HN
∴ ON2-OM2=(ON+OM)(ON-OM)
=[(OH+HN)+(OH-MH)][(OH+HN)-(OH-MH)]
=(2OH)(HN+MH)
=(2OH)(2AH)
=4OH ![]() AH
AH
4x12 =48
点睛: 本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.


科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上(E不与A、B重合),连接EF、CF,则下列结论中一定成立的是 ( )
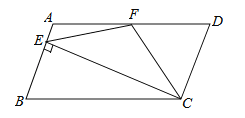
①∠DCF=![]() ∠BCD;②EF=CF;③
∠BCD;②EF=CF;③![]() ;④∠DFE=4∠AEF.
;④∠DFE=4∠AEF.
A. ①②③④ B. ①②③ C. ①② D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF

(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=8,CE=![]() ,求□ABCD的面积.
,求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得
不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得![]() 成立的一对数m,n为“相伴数对”,记为(m,n).
成立的一对数m,n为“相伴数对”,记为(m,n).
(1)若(m,1)是“相伴数对”,则m=_____;
(2)(m,n)是“相伴数对”,则代数式![]() m﹣[n+
m﹣[n+![]() (6﹣12n﹣15m)]的值为_____.
(6﹣12n﹣15m)]的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人从少年宫出发,沿相同的路线分别以不同的速度匀速跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象.
(1)在跑步的全过程中,甲共跑了米,甲的速度为米/秒;
(2)乙跑步的速度是多少?乙在途中等候甲用了多长时间?
(3)甲出发多长时间第一次与乙相遇?此时乙跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )

A. 10 B. 8 C. 14 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5,-2,1,9,且任意相邻四个台阶上数的和都相等.
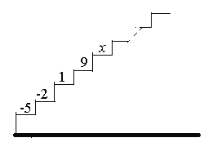
(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数![]() 是多少?
是多少?
(3)从下到上前多少个台阶上数的和为30.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
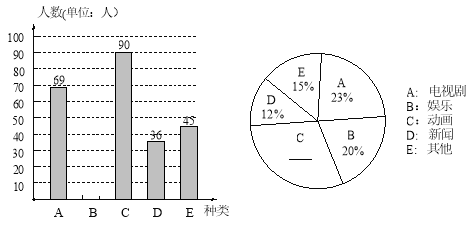
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有2000名学生,请估计该校喜爱电视剧节目的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com