
����Ŀ����̽�����֡�
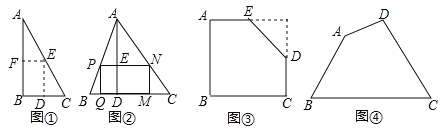
��ͼ������һ��ֱ��������ֽƬ����B=60�㣬С������м���һ������BΪ�ڽ���������ľ��Σ�������β������֣���������λ��DE��EF����ʱ�����õľ��ε������������ͨ��֤����֤������ȷ�ԣ����ó������ε���������ԭ����������ı�ֵΪ ��
����չӦ�á�
��ͼ��������ABC�У�BC=a��BC���ϵĸ�AD=h������PQMN�Ķ���P��N�ֱ��ڱ�AB��AC�ϣ�����Q��M�ڱ�BC�ϣ������PQMN��������ֵΪ �����ú�a��h�Ĵ���ʽ��ʾ��
�����Ӧ�á�
��ͼ������һ�顰ȱ�Ǿ��Ρ�ABCDE��AB=32��BC=40��AE=20��CD=16��С�����м�����һ��������ľ��Σ���BΪ���������ε��ڽǣ�����þ��ε������
��ʵ��Ӧ�á�
��ͼ��������һ���ı��ε�ľ������ABCD��������AB=50cm��BC=108cm��CD=60cm����tanB=tanC=![]() ��ľ����ʦ������������вó��˶���M��N�ڱ�BC����������ľ���PQMN����þ��ε������
��ľ����ʦ������������вó��˶���M��N�ڱ�BC����������ľ���PQMN����þ��ε������
���𰸡���̽�����֡�![]() ������չӦ�á�
������չӦ�á�![]() �������Ӧ�á�720����ʵ��Ӧ�á�1944��
�������Ӧ�á�720����ʵ��Ӧ�á�1944��
��������
�����������̽�����֡�������λ��֪EF=![]() BC��ED=
BC��ED=![]() AB����
AB����![]() =
=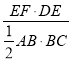 �ɵã�
�ɵã�
����չӦ�á�������APN�ס�ABC֪![]() ���ɵ�PN=a��
���ɵ�PN=a��![]() PQ����PQ=x����S����PQMN=PQPN�T
PQ����PQ=x����S����PQMN=PQPN�T![]() ���ݴ˿ɵã�
���ݴ˿ɵã�
�����Ӧ�á���������ͼ1�����ߣ�ȡBF�е�I��FG���е�K���ɾ�������֪AE=EH20��CD=DH=16���ֱ�֤��AEF�ա�HED����CDG�ա�HDE��AF=DH=16��CG=HE=20���Ӷ��жϳ���λ��IK�����˵����߶�AB��DE�ϣ����á�̽�����֡����۽�ɣ�
��ʵ��Ӧ�á����ӳ�BA��CD���ڵ�E������E��EH��BC�ڵ�H����tanB=tanC֪EB=EC��BH=CH=54��EH=![]() BH=72���̶����BE=CE=90�����ж���λ��PQ�����˵����߶�AB��CD�ϣ����á���չӦ�á����۽��ɵã�
BH=72���̶����BE=CE=90�����ж���λ��PQ�����˵����߶�AB��CD�ϣ����á���չӦ�á����۽��ɵã�
�����������̽�����֡�
��EF��EDΪ��ABC��λ�ߣ���ED��AB��EF��BC��EF=![]() BC��ED=
BC��ED=![]() AB������B=90�㣬���ı���FEDB�Ǿ��Σ���
AB������B=90�㣬���ı���FEDB�Ǿ��Σ���![]() =
=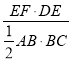 =
=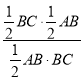 =
=![]() ���ʴ�Ϊ��
���ʴ�Ϊ��![]() ��
��
����չӦ�á�
��PN��BC�����APN�ס�ABC����![]() ����
����![]() ����PN=a��
����PN=a��![]() PQ����PQ=x����S����PQMN=PQPN=x��a��
PQ����PQ=x����S����PQMN=PQPN=x��a��![]() x��=
x��=![]() =
=![]() ������PQ=
������PQ=![]() ʱ��S����PQMN���Ϊ
ʱ��S����PQMN���Ϊ![]() ���ʴ�Ϊ��
���ʴ�Ϊ��![]() ��
��
�����Ӧ�á�
��ͼ1���ӳ�BA��DE���ڵ�F���ӳ�BC��ED���ڵ�G���ӳ�AE��CD���ڵ�H��ȡBF�е�I��FG���е�K��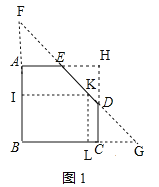
������֪�ı���ABCH�Ǿ��Σ���AB=32��BC=40��AE=20��CD=16����EH=20��DH=16����AE=EH��CD=DH������AEF����HED�У��ߡ�FAE=��DHE��AE=AH����AEF=��HED�����AEF�ա�HED��ASA������AF=DH=16��ͬ����CDG�ա�HDE����CG=HE=20����BI=![]() ��AB+AF��=24����BI=24��32������λ��IK�����˵����߶�AB��DE�ϣ�����K��KL��BC�ڵ�L���ɡ�̽�����֡�֪���ε�������Ϊ
��AB+AF��=24����BI=24��32������λ��IK�����˵����߶�AB��DE�ϣ�����K��KL��BC�ڵ�L���ɡ�̽�����֡�֪���ε�������Ϊ![]() ��BGBF=
��BGBF=![]() ����40+20������32+16��=720���𣺸þ��ε����Ϊ720��
����40+20������32+16��=720���𣺸þ��ε����Ϊ720��
��ʵ��Ӧ�á�
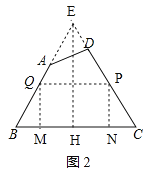
��ͼ2���ӳ�BA��CD���ڵ�E������E��EH��BC�ڵ�H����tanB=tanC=![]() �����B=��C����EB=EC����BC=108cm����EH��BC����BH=CH=
�����B=��C����EB=EC����BC=108cm����EH��BC����BH=CH=![]() BC=54cm����tanB=
BC=54cm����tanB=![]() =
=![]() ����EH=
����EH=![]() BH=
BH=![]() ��54=72cm����Rt��BHE��BE=
��54=72cm����Rt��BHE�У�BE=![]() =90cm����AB=50cm����AE=40cm����BE���е�Q���߶�AB�ϣ���CD=60cm����ED=30cm����CE���е�P���߶�CD�ϣ�����λ��PQ�����˵����߶�AB��CD�ϣ��ɡ���չӦ�á�֪������PQMN��������Ϊ
=90cm����AB=50cm����AE=40cm����BE���е�Q���߶�AB�ϣ���CD=60cm����ED=30cm����CE���е�P���߶�CD�ϣ�����λ��PQ�����˵����߶�AB��CD�ϣ��ɡ���չӦ�á�֪������PQMN��������Ϊ![]() BCEH=1944cm2��
BCEH=1944cm2��
�𣺸þ��ε����Ϊ1944cm2��


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AOB��100������BOC��60����OMƽ�֡�AOB��ONƽ�֡�BOC�����MON�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������A��B�����Ӧ�����ֱ�Ϊ��2��8��PΪ����������һ���Ҷ�Ӧ����Ϊx��CΪ�߶�PA���е㣮
��1������P���߶�AB�ϣ���2BC��BP��ֵ��
��2������P���߶�AB���ӳ����ϣ�ʽ��2BC��BP��ֵ�Ƕ�ֵ�����ǣ��������ֵ�������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
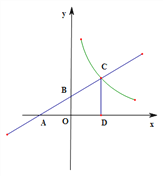
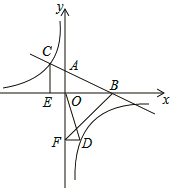
����Ŀ����֪һ�κ���![]() ��ͼ��ֱ����������ཻ��A��B���㣨��ͼ��ʾ�����뷴��������
��ͼ��ֱ����������ཻ��A��B���㣨��ͼ��ʾ�����뷴��������![]() ��ͼ���ཻ�ڵ�C��OA=3.
��ͼ���ཻ�ڵ�C��OA=3.
��1����һ�κ����Ľ���ʽ�͵�B�����ꣻ
��2����CD��x�ᣬ����ΪD����![]() =1:3����������
=1:3����������![]() �Ľ���ʽ.
�Ľ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2013��1��1���½�ͨ���濪ʼʵʩ��Ϊ�˽�ij�����������ؽ�ͨ���������С�����ѡȡ���־���������˴���������������ʾ����飬�����Ϊ��A���Ӳ�����ƣ�B��ż������ƣ�C����������ƣ�D����������������������ݵ��������Ƴ���������ͳ��ͼ����ͼ1���Ͳ�������ͳ��ͼ����ͼ2���������ͼ����Ϣ������������⣺
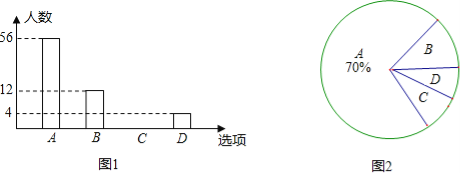
��1�����ε��鹲ѡȡ�� ��������
��2���������ͳ��ͼ����C���������ε�Բ�ĽǵĶ�������������ͳ��ͼ����������
��3��������������о���1600�ˣ������ж����˴Ӳ�����ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BAC=90����AB=4��AC=6����D��E�ֱ���BC��AD���е㣬AF��BC��CE���ӳ�����F�����ı���AFBD�����Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ύ�ڵ�B����y�ύ�ڵ�A���뷴��������y��![]() ��ͼ���ڵڶ������ڵ�C��CE��x�ᣬ����Ϊ��E��tan��ABO��
��ͼ���ڵڶ������ڵ�C��CE��x�ᣬ����Ϊ��E��tan��ABO��![]() ��OB��4,OE��2��
��OB��4,OE��2��
��1�����������Ľ���ʽ��
��2������D�Ƿ���������ͼ���ڵ��������ϵĵ㣬����D��DF��y�ᣬ����Ϊ��F������OD��BF�����S��BAF��4S��DFO�����D������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�г��Ĺ�ƽ����ͼ,��10ǧ�˵IJ˷ŵ�����,ָʾ���ϵ�ָ��ת��180��.
(1)�����2.75ǧ�˵IJ˷��ڳ���,ָ��ת�����ٶ�?
(2)����ƺ�0.5ǧ�˵IJ�û������,�ٰ�һ���˷��ڳ���,ָ�빲ת��![]() ��ô,����ϵ��������ж���ǧ��?
��ô,����ϵ��������ж���ǧ��?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com