练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知为线段上一点，为的中点，为的中点，为的中点.若，则___________.

    【答案】或

    【解析】

    由题意设AC=x，BC=y，易得DE=DC+CE=（x+y），再计算出DF=DE=（x+y），讨论：当AC＜BC，CF=DF-DC=（y-x），接着利用AB=16CF得到x+y=16（y-x），化简后有5x=3y，然后利用比例性质即可得到的值；当AC＞BC时，同样方法可得=.

    解：设AC=x，BC=y，则DC=AC=x，CE=BC=y，

    ∴DE=DC+CE=（x+y），

    ∵F为DE的中点，

    ∴DF=DE=（x+y），

    当AC＜BC时，

    ∴CF=DF-DC=（x+y）-x=（y-x）；

    ∵AB=16CF，

    ∴x+y=16（y-x），

    ∴5x=3y，

    ∴，

    当AC＞BC．

    ∴CF=DC-DF=x-（x+y）=（x-y）；

    ∵AB=16CF，

    ∴x+y=16（x-y），

    ∴3x=5y，

    ∴，

    综上所述，或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校八年级共有800名学生，准备调查他们对“低碳”知识的了解程度．

    （1）在确定调查方式时，团委设计了以下三种方案：

    方案一：调查八年级部分女生；

    方案二：调查八年级部分男生；

    方案三：到八年级每个班去随机调查一定数量的学生．

    请问其中最具有代表性的一个方案是_____；

    （2）团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图（如图①、图②所示），请你根据图中信息，将两个统计图补充完整；

    （3）请你估计该校八年级约有多少名学生比较了解“低碳”知识．

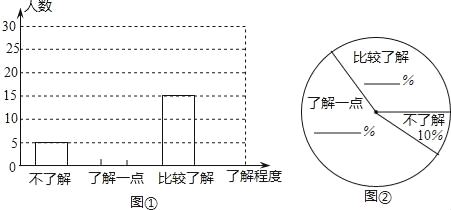
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】列方程解应用题：

    周末，小明从城里去渡假村接父母回家，为了欣赏路边的风景，小明从城里步行出发，同时父母也从渡假村步行出发，相向而行，城里距渡假村，小明每小时走，父母每小时走，如果小明带一只狗和他同时出发，狗以每小时的速度向父母方向跑去，遇到父母后又立即回头跑向小明，遇到小明后又立即回头跑向父母，这样往返直到二人相遇.

    （1）小明与父母经过多少小时相遇？

    （2）这只狗共跑了多少呢？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是直线上一点，平分，.则图中互余的角、互补的角各有（ ）对

    A.4，7B.4，4C.4，5D.3，3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校准备购进一批节能灯，已知2只型节能灯和5只型节能灯共需45元；4只型节能灯和3只型节能灯共需41元.

    (1)求一只型节能灯和一只型节能灯的售价各是多少元.

    (2)学校准备购进这两种型号的节能灯共50只，并且型节能灯的数量不多于型节能灯数量的3倍，请设计出最省钱的购买方案，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，点为平面内一点.

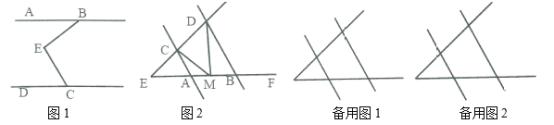
    （1）如图1，和互余，小明说过作，很容易说明。请帮小明写出具体过程；

    （2）如图2，，当点在线段上移动时（点与，两点不重合），指出与，的数量关系？请说明理由；

    （3）在（2）的条件下，若点在，两点外侧运动（点与，，三点不重合）请直接写出与，的数量关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【探索发现】

    如图①，是一张直角三角形纸片，∠B=60°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为 ．

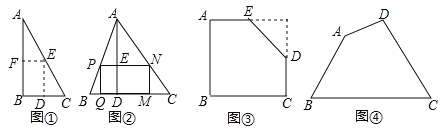
    【拓展应用】

    如图②，在△ABC中，BC=a，BC边上的高AD=h，矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，则矩形PQMN面积的最大值为 ．（用含a，h的代数式表示）

    【灵活应用】

    如图③，有一块“缺角矩形”ABCDE，AB=32，BC=40，AE=20，CD=16，小明从中剪出了一个面积最大的矩形（∠B为所剪出矩形的内角），求该矩形的面积．

    【实际应用】

    如图④，现有一块四边形的木板余料ABCD，经测量AB=50cm，BC=108cm，CD=60cm，且tanB=tanC=，木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN，求该矩形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一般情况下不成立，但有些数可以使得它成立，例如：m=n=0时，我们称使得成立的一对数m，n为“相伴数对”，记为（m，n）．

    （1）若（m，1）是“相伴数对”，则m=_____；

    （2）（m，n）是“相伴数对”，则代数式m﹣[n+（6﹣12n﹣15m）]的值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

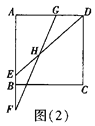
    【题目】如图，四边形ABCD为正方形，点E在边 AB上，点F在AB的延长线上，点G在边AD上，且EF= AB，DG= AE，连接DE、FG相交于点H.

    (1)若，如图(1)，求∠EHF的度数（提示：连接CG，CF）；

    (2)若，如图(2)，求tan∠EHF的值．

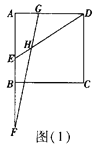
    查看答案和解析>>

    同步练习册答案