
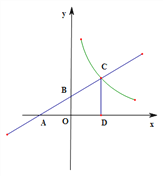
【题目】已知一次函数![]() 的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数
的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数![]() 的图象相交于点C,OA=3.
的图象相交于点C,OA=3.
(1)求一次函数的解析式和点B的坐标;
(2)作CD⊥x轴,垂足为D,若![]() =1:3,求反比例函数
=1:3,求反比例函数![]() 的解析式.
的解析式.
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
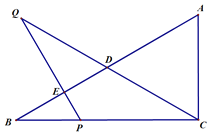
【题目】已知,如图, 在![]() 中,
中, ![]() ,
,![]() ,
,![]() ,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC, 联结
,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC, 联结![]() 交边AB于点
交边AB于点![]() .
.
(1)求AD的长;
(2)设![]() ,
,![]() 的面积为y, 求y关于x的函数解析式,并写出定义域;
的面积为y, 求y关于x的函数解析式,并写出定义域;
(3)过点C作![]() , 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时,
, 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时,![]() 为等边三角形?请指出点P的位置并加以证明.
为等边三角形?请指出点P的位置并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察表格:
|
|
| |
1条直线 0个交点 平面分成(1+1)块 | 2条直线 1个交点 平面分成(1+1+2)块 | 3条直线 (1+2)个交点 平面分成(1+1+2+3)块 | 4条直线 (1+2+3)个交点 平面分成(1+1+2+3+4)块 |
根据表格中的规律解答问题:
(1)5条直线两两相交,有 个交点,平面被分成 块;
(2)n条直线两两相交,有 个交点,平面被分成 块;
(3)应用发现的规律解决问题:一张圆饼切10刀(不许重叠),最多可得到 块饼.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知2只![]() 型节能灯和5只
型节能灯和5只![]() 型节能灯共需45元;4只
型节能灯共需45元;4只![]() 型节能灯和3只
型节能灯和3只![]() 型节能灯共需41元.
型节能灯共需41元.
(1)求一只![]() 型节能灯和一只
型节能灯和一只![]() 型节能灯的售价各是多少元.
型节能灯的售价各是多少元.
(2)学校准备购进这两种型号的节能灯共50只,并且![]() 型节能灯的数量不多于
型节能灯的数量不多于![]() 型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探索发现】
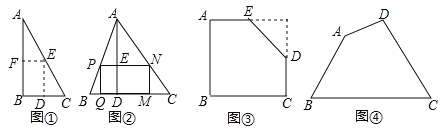
如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小虫从点A出发在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的路程依次为:(单位:cm)①+5,②-3,③+10,④-8,⑤-6,⑥+11,⑦-9.
(1)小虫最后是否回到出发点A,说明理由;
(2)小虫在第几次爬行后离点A最远,此时距离点A多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,那么小虫一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
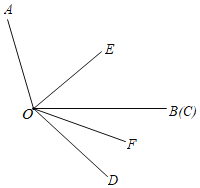
【题目】已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.
(1)如图,求∠EOF的度数.
(2)如图,当OB、OC重合时,求∠AOE﹣∠BOF的值;
(3)当∠COD从图的位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )
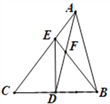
A. 1个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com