
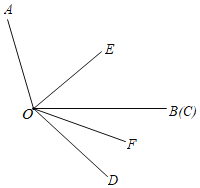
����Ŀ����֪��AOB��110������COD��40����OEƽ�֡�AOC��OFƽ�֡�BOD��
��1����ͼ�����EOF�Ķ�����
��2����ͼ����OB��OC�غ�ʱ�����AOE����BOF��ֵ��
��3������COD��ͼ��λ���Ƶ�O��ÿ��3�����ٶ�˳ʱ����תt�루0��t��10��������ת�����С�AOE����BOF��ֵ�Ƿ����t�ı仯���仯�����������仯��������ö�ֵ���������仯����˵�����ɣ�
���𰸡���1����EOF��75������2����AOE����BOF��35������3����AOE����BOF=35��.
��������
��1��ֱ�����ý�ƽ���ߵ����������EOC�͡�COF����Ӽ�������𰸣�
��2�����ý�ƽ���ߵ����������AOE�͡�COF�������������𰸣�
��3����OC����O˳ʱ����תʱ����AOB�DZ仯�ģ���AOB=110��+3��t����BOD�Dz��仯�ģ����ԡ�AOE-��BOFֵ�Dz��仯�ģ�
��1����OEƽ�֡�AOC��OFƽ�֡�BOD��
���EOF����EOB+��BOF��![]() ��AOB+
��AOB+![]() ��BOD��
��BOD��
�ߡ�AOB��110������COD��40����
���EOF��75����
��2����OEƽ�֡�AOC��OFƽ�֡�BOD����AOB��110������COD��40����
���AOE��55������BOF��20����
���AOE����BOF��35����
��3����OFƽ�֡�BOD��
���BOF��![]() ��BOD��
��BOD��
�ߡ�AOB��110����BO���Ƶ�O��ÿ��3�����ٶ�˳ʱ����תt�룬
���AOB��110��+3��t����BOF��![]() ��40��+3��t����
��40��+3��t����
��OEƽ�֡�AOB��
���AOE��![]() ��110��+3��t����
��110��+3��t����
���AOE����BOF��![]() ��110��+3��t����20����
��110��+3��t����20����![]() t��35����
t��35����
������ת�����С�AOE����BOF��ֵ�Dz�����t�ı仯���仯����AOE����BOF��35����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��ֱ��
��ֱ��![]() ����һ�㣬����
����һ�㣬����![]() ������
������![]() �ֱ�ƽ��
�ֱ�ƽ��![]() ��
��![]() .
.
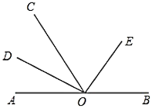
��1����գ���![]() �����Ľ���______��
�����Ľ���______��
��2����![]() ����
����![]() �Ķ�����
�Ķ�����
��3����![]() ʱ����ֱ��д��
ʱ����ֱ��д��![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
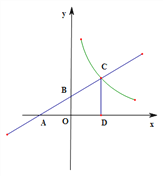
����Ŀ����֪һ�κ���![]() ��ͼ��ֱ����������ཻ��A��B���㣨��ͼ��ʾ�����뷴��������
��ͼ��ֱ����������ཻ��A��B���㣨��ͼ��ʾ�����뷴��������![]() ��ͼ���ཻ�ڵ�C��OA=3.
��ͼ���ཻ�ڵ�C��OA=3.
��1����һ�κ����Ľ���ʽ�͵�B�����ꣻ
��2����CD��x�ᣬ����ΪD����![]() =1:3����������
=1:3����������![]() �Ľ���ʽ.
�Ľ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BAC=90����AB=4��AC=6����D��E�ֱ���BC��AD���е㣬AF��BC��CE���ӳ�����F�����ı���AFBD�����Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
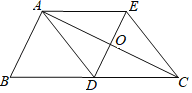
����Ŀ����ͼ����֪��ABC�У�AD�DZ�BC�ϵ����ߣ�����A��AE��BC������D��DE��AB��DE��AC��AE�ֱ��ڵ�O����E������EC��
��1����֤���ı���ADCE��ƽ���ı��Σ�
��2������BAC��90��ʱ����֤���ı���ADCE�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ύ�ڵ�B����y�ύ�ڵ�A���뷴��������y��![]() ��ͼ���ڵڶ������ڵ�C��CE��x�ᣬ����Ϊ��E��tan��ABO��
��ͼ���ڵڶ������ڵ�C��CE��x�ᣬ����Ϊ��E��tan��ABO��![]() ��OB��4,OE��2��
��OB��4,OE��2��
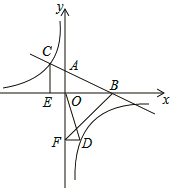
��1�����������Ľ���ʽ��
��2������D�Ƿ���������ͼ���ڵ��������ϵĵ㣬����D��DF��y�ᣬ����Ϊ��F������OD��BF�����S��BAF��4S��DFO�����D������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
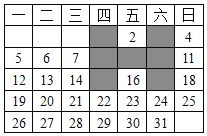
����Ŀ����ͼ�����и�������ij�µ�����������ѡȡ��![]() ���Ϳ��е�
���Ϳ��е�![]() ����(����Ӱ������ʾ).����������ѧ����ѧ֪ʶ���о�������
����(����Ӱ������ʾ).����������ѧ����ѧ֪ʶ���о�������![]() �����ĺͲ������ǣ� ��
�����ĺͲ������ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A��B��C���������������ֱ���a��b��1����|a��1|��|1��b|��|a��b|�������ĸ�ѡ���У��У����������ܱ�ʾA��B��C�����������ϵ�λ�ù�ϵ��
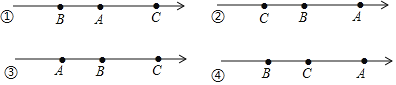
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
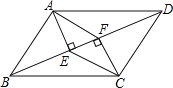
����Ŀ����ͼ�����ı���ABCD�У�AB��CD��BF=DE,AE��BD��CF��BD������ֱ�ΪE��F��
(1)��֤����ABE�ա�CDF��
(2)��AC��BD���ڵ�O����֤��AC��BD����ƽ�֣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com