
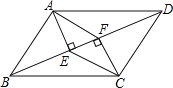
【题目】如图,在四边形ABCD中,AB∥CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AC与BD互相平分.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
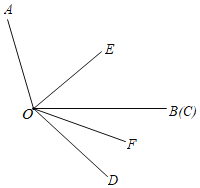
【题目】已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.
(1)如图,求∠EOF的度数.
(2)如图,当OB、OC重合时,求∠AOE﹣∠BOF的值;
(3)当∠COD从图的位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )
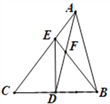
A. 1个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E. F,垂足为O.

(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A. C两点同时出发,沿△AFB和△CDE各边匀速运动一周。即点P自A→F→B→A停止,点Q自C→D→E→C停止。在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.
①问在运动的过程中,以A. P、C. Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.
②若点Q的速度为每秒0.8cm,当A. P、C. Q四点为顶点的四边形是平行四边形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
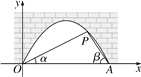
【题目】图中是抛物线型拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α,β,tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少(![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD,OE分别是∠AOC,∠BOC的角平分线,下列叙述正确的是( )

A. ∠AOD+∠BOE=60°B. ∠AOD=![]() ∠EOC
∠EOC
C. ∠BOE=2∠CODD. ∠DOE的度数不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:|﹣6|﹣7+(﹣3)
(2)计算:﹣32÷3﹣![]() ×(﹣2)3
×(﹣2)3
(3)化简:2(2x2y+x)﹣3(x2y﹣2x)
(4)解方程:5﹣2x=3(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com