
【题目】如图,点![]() 是直线
是直线![]() 上任一点,射线
上任一点,射线![]() 和射线
和射线![]() 分别平分
分别平分![]() 和
和![]() .
.
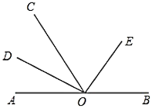
(1)填空:与![]() 互补的角有______;
互补的角有______;
(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)当![]() 时,请直接写出
时,请直接写出![]() 的度数.
的度数.
【答案】(1)∠AOD、∠COD;(2)90°;(3)90°.
【解析】
(1)先根据角平分线的定义得出∠AOD=∠COD,再由∠AOD+∠BOD=180°,即可得出答案;
(2)根据补角的定义和角平分线的定义求出∠COE,即可得出∠DOE;
(3)根据角平分线的定义和补角的定义依次求出∠EOC和∠DOC,即可得出∠DOE.
解:(1)∵OD平分∠AOC,∴∠AOD=∠COD;
∵∠AOD+∠BOD=180°,∴∠COD+∠BOD=180°,
∴与∠BOD互补的角是∠AOD和∠COD;
故答案为∠AOD、∠COD;
(2)∵OD、OE分别平分∠AOC、∠BOC,
∴∠COD=∠AOD=26°,∠COE=∠BOE=![]() ∠BOC,
∠BOC,
∴∠AOC=2×26°=52°,∴∠BOC=180°-52°=128°,
∴∠COE=![]() ∠BOC=64°,
∠BOC=64°,
∴∠DOE=∠COD+∠COE=90°;
(3)当![]() 时,∠DOE=90°.
时,∠DOE=90°.
理由:∵OE平分∠BOC,∴∠COE=∠BOE=![]() ∠BOC=
∠BOC=![]() ,
,
∴∠BOC=2![]() ,∴
,∴![]() ,
,
∵OD平分∠AOC,∴∠COD =![]() ∠AOC=
∠AOC=![]() ,
,
∴∠DOE=∠EOC+∠DOC=![]() +
+![]() =
=![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图, 在![]() 中,
中, ![]() ,
,![]() ,
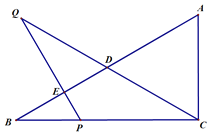
,![]() ,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC, 联结
,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC, 联结![]() 交边AB于点
交边AB于点![]() .
.
(1)求AD的长;
(2)设![]() ,
,![]() 的面积为y, 求y关于x的函数解析式,并写出定义域;
的面积为y, 求y关于x的函数解析式,并写出定义域;
(3)过点C作![]() , 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时,
, 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时,![]() 为等边三角形?请指出点P的位置并加以证明.
为等边三角形?请指出点P的位置并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: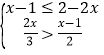 , 并把解集在数轴上表示出来.
, 并把解集在数轴上表示出来.
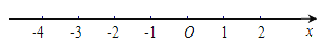
【答案】-3<x≤1
【解析】分析:分别解不等式,在数轴上表示出解集,找出解集的公共部分即可.
详解: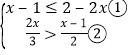 ,
,
解不等式①得:![]() ,
,
解不等式②得:![]()
∴原不等式组的解集为-3<x≤1
解集在数轴上表示为:

点睛:考查解一元一次不等式组,比较容易,分别解不等式,找出解集的公共部分即可.
【题型】解答题
【结束】
17
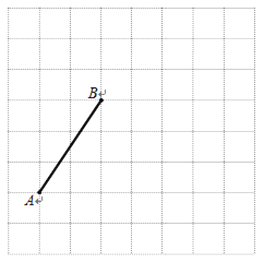
【题目】下图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.
(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(-3,-1),在此坐标系下,B点的坐标为________________;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为__________________;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c(a≠0)的图象过O、B、C三点,则此函数图象的对称轴方程是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
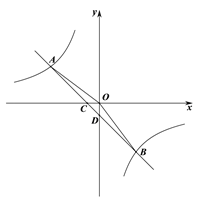
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数图象交于第二,四象限内A,B两点,与![]() 轴交于点C,与
轴交于点C,与![]() 轴交于点D.若点B的纵坐标为
轴交于点D.若点B的纵坐标为![]() ,OA=5,
,OA=5, ![]() .
.
(1)求反比例函数解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
周末,小明从城里去渡假村接父母回家,为了欣赏路边的风景,小明从城里步行出发,同时父母也从渡假村步行出发,相向而行,城里距渡假村![]() ,小明每小时走
,小明每小时走![]() ,父母每小时走
,父母每小时走![]() ,如果小明带一只狗和他同时出发,狗以每小时
,如果小明带一只狗和他同时出发,狗以每小时![]() 的速度向父母方向跑去,遇到父母后又立即回头跑向小明,遇到小明后又立即回头跑向父母,这样往返直到二人相遇.
的速度向父母方向跑去,遇到父母后又立即回头跑向小明,遇到小明后又立即回头跑向父母,这样往返直到二人相遇.
(1)小明与父母经过多少小时相遇?
(2)这只狗共跑了多少![]() 呢?
呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察表格:
|
|
| |
1条直线 0个交点 平面分成(1+1)块 | 2条直线 1个交点 平面分成(1+1+2)块 | 3条直线 (1+2)个交点 平面分成(1+1+2+3)块 | 4条直线 (1+2+3)个交点 平面分成(1+1+2+3+4)块 |
根据表格中的规律解答问题:
(1)5条直线两两相交,有 个交点,平面被分成 块;
(2)n条直线两两相交,有 个交点,平面被分成 块;
(3)应用发现的规律解决问题:一张圆饼切10刀(不许重叠),最多可得到 块饼.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知2只![]() 型节能灯和5只
型节能灯和5只![]() 型节能灯共需45元;4只
型节能灯共需45元;4只![]() 型节能灯和3只
型节能灯和3只![]() 型节能灯共需41元.
型节能灯共需41元.
(1)求一只![]() 型节能灯和一只
型节能灯和一只![]() 型节能灯的售价各是多少元.
型节能灯的售价各是多少元.
(2)学校准备购进这两种型号的节能灯共50只,并且![]() 型节能灯的数量不多于
型节能灯的数量不多于![]() 型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
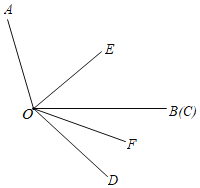
【题目】已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.
(1)如图,求∠EOF的度数.
(2)如图,当OB、OC重合时,求∠AOE﹣∠BOF的值;
(3)当∠COD从图的位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com