
【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,![]() cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)

【答案】t=2或3≤t≤7或t=8。
【解析】∵△ABC是等边三角形,∴AB=AC=BC=AM+MB=4cm,∠A=∠C=∠B=60°。
∵QN∥AC,AM=BM.∴N为BC中点。
∴MN=![]() AC=2cm,∠BMN=∠BNM=∠C=∠A=60°。
AC=2cm,∠BMN=∠BNM=∠C=∠A=60°。
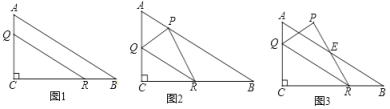
分为三种情况:①如图1,当⊙P切AB于M′时,连接PM′,
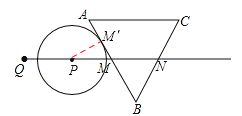
则PM′=![]() cm,∠PM′M=90°,
cm,∠PM′M=90°,
∵∠PMM′=∠BMN=60°,∴M′M=1cm,PM=2MM′=2cm,
∴QP=4cm﹣2cm=2cm,
∵速度是每秒1cm,∴t=2。
②如图2,当⊙P于AC切于A点时,连接PA,
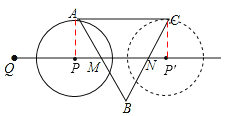
则∠CAP=∠APM=90°,∠PMA=∠BMN=60°,AP=![]() cm
cm
∴PM=1cm,∴QP=4cm﹣1cm=3cm。
∵速度是每秒1cm,∴t=3。
当⊙P于AC切于C点时,连接P′C,
则∠CP′N=∠ACP′=90°,∠P′NC=∠BNM=60°,CP′=![]() cm,
cm,
∴P′N=1cm,∴QP=4cm+2cm+1cm=7cm。
∵速度是每秒1cm,∴t=7。
∴当3≤t≤7时,⊙P和AC边相切。
③如图3,当⊙P切BC于N′时,连接PN′,
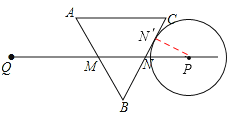
则PN′=![]() cm,∠PM\N′N=90°,
cm,∠PM\N′N=90°,
∵∠PNN′=∠BNM=60°,∴N′N=1cm,PN=2NN′=2cm。
∴QP=4cm+2cm+2cm=8cm。
∵速度是每秒1cm,∴t=8。
综上所述,t可取的一切值为:t=2或3≤t≤7或t=8。


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2![]() ,延长AD到E,使AE=2AD,连接BE.
,延长AD到E,使AE=2AD,连接BE.
(1)求证:△ABE为等边三角形;
(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60°,边NE与AB交于点G,边ME与AC交于点F.求证:BG=AF;
(3)在(2)的条件下,求四边形AGEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学期末,某班评选一名优秀学生干部,下表是班长、学习委员和团支部书记的得分情况:

假设在评选优秀干部时,思想表现、学习成绩、工作能力这三方面的重要比为3 ∶3 ∶4 ,通过计算说明谁应当选为优秀学生干部。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接BF,则图中阴影部分的面积是_____.
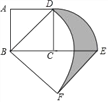
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一定是一元二次方程的有( )
(1)(a-1)x+bx+c=0(a,b,c是实数);(2)2x+![]() +3=0;(3)(1-2x)(3-x)=2x+1;(4)x+2x-y=0;(5)
+3=0;(3)(1-2x)(3-x)=2x+1;(4)x+2x-y=0;(5)![]() x-8=
x-8=![]() x
x
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据直尺和三角尺的实物摆放图,解决下列问题.



(1)如图1,是我们学过的用直尺和三角尺画平行线的方法的示意图,画图的原理是__________;
(2)如图2,图中互余的角有________________,若要使直尺的边缘DE与三角尺的AB边平行,则应满足_________(填角相等);
(3)如图3,若BC∥GH,试判断AC和FG的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,AB=4,点
,AB=4,点![]() 是边
是边![]() 上动点(点
上动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ,交
,交![]() 边于点
边于点![]() .
.
(1)求![]() 的大小;
的大小;
(2)若把![]() 沿着直线
沿着直线![]() 翻折得到
翻折得到![]() ,设
,设![]()
① 如图2,当点![]() 落在斜边
落在斜边![]() 上时,求
上时,求![]() 的值;
的值;
② 如图3,当点![]() 落在
落在![]() 外部时,
外部时,![]() 与
与![]() 相交于点
相交于点![]() ,如果
,如果![]() ,写出
,写出![]() 与
与![]() 的函数关系式以及定义域.
的函数关系式以及定义域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com