
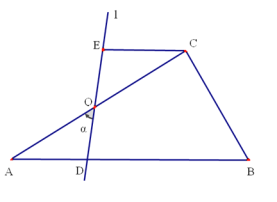
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点O是
.点O是![]() 的中点,过点O的直线
的中点,过点O的直线![]() 与从
与从![]() 重合的位置开始,绕点O作逆时针旋转,交
重合的位置开始,绕点O作逆时针旋转,交![]() 于点D,过点C作
于点D,过点C作![]() 交直线
交直线![]() 于点E,设直线
于点E,设直线![]() 的旋转角为
的旋转角为![]() .
.
(1)当四边形![]() 是等腰梯形时,则
是等腰梯形时,则![]() =_______,此时
=_______,此时![]() ________;
________;
(2)当四边形![]() 是直角梯形时,则
是直角梯形时,则![]() =_________,此时
=_________,此时![]() _________;
_________;
(3)当![]() 为几度时,判断四边形
为几度时,判断四边形![]() 是否为菱形,并说明理由.
是否为菱形,并说明理由.
【答案】(1)![]() ,1;(2)
,1;(2)![]() ,
,![]() ;(3)
;(3)![]() ,理由详见解析
,理由详见解析
【解析】
(1)根据旋转的性质和等腰梯形的性质,由![]() ,可得当
,可得当![]() 时,四边形EDBC是等腰梯形,即可求得
时,四边形EDBC是等腰梯形,即可求得![]() 的度数,然后利用含30°角的直角三角形的性质与等腰三角形三线合一的性质求得AD的长;
的度数,然后利用含30°角的直角三角形的性质与等腰三角形三线合一的性质求得AD的长;
(2)由![]() ,可得当
,可得当![]() 时,四边形EDBC是直角梯形,即可求得
时,四边形EDBC是直角梯形,即可求得![]() 的度数,然后利用含30°角的直角三角形的性质与勾股定理求得AD的长;
的度数,然后利用含30°角的直角三角形的性质与勾股定理求得AD的长;
(3)根据![]() ,先证明四边形
,先证明四边形![]() 是平行四边形,再利用在Rt△ABC中,
是平行四边形,再利用在Rt△ABC中,![]() ,
,![]() ,求得AB、AC、AO的长度,在Rt△AOD中,
,求得AB、AC、AO的长度,在Rt△AOD中,![]() ,求得BD的长度,比较得
,求得BD的长度,比较得![]() ,可证得四边形
,可证得四边形![]() 是菱形.
是菱形.
(1)∵![]()
∴当![]() 时,四边形EDBC是等腰梯形
时,四边形EDBC是等腰梯形
∵![]()
∴![]()
即当![]() 时,四边形EDBC是等腰梯形
时,四边形EDBC是等腰梯形
在Rt△ABC中,![]()
∴![]()
∴![]()
∵O是AC的中点
∴![]()
∵![]()
∴![]() ;
;
(2)∵![]()
∴当![]() 时,四边形EDBC是直角梯形
时,四边形EDBC是直角梯形
∵![]()
∴![]()
∴当![]() 时,四边形EDBC是直角梯形
时,四边形EDBC是直角梯形
在Rt△ABC中,![]()
∴![]()
∴![]()
∵O是AC的中点
∴![]()
在Rt△AOD中,![]()
∴![]() ;
;
(3)当![]() 时,四边形
时,四边形![]() 是菱形
是菱形
∵![]()
∴![]()
∵![]()
∴四边形![]() 是平行四边形
是平行四边形
在Rt△ABC中,![]() ,
,![]()
∴![]()
∴![]()
∴![]()
在Rt△AOD中,![]()

∴![]()
∴![]()
∴![]()
∵四边形![]() 是平行四边形
是平行四边形
∴四边形![]() 是菱形.
是菱形.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=![]() AB中,一定正确的是( )
AB中,一定正确的是( )
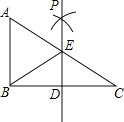
A.①②③ B.①②④ C.①③④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利80元.为了扩大销售、尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价5元,商场平均每天就能多售出2件.请解答下列问题:
(1)当每件衬衫降价30元时,求商场每天销售该衬衫所获得的总利润.
(2)当该衬衫每件降价多少元时,商场销售该衬衫每天所获得的利润为1680元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是![]() ,连接
,连接![]() 交于点O,并分别与边
交于点O,并分别与边![]() 交于点
交于点![]() ,连接AE,下列结论:
,连接AE,下列结论: ![]() ;
; ![]() ;
; ![]() ;
; ![]() 当
当![]() 时,
时, ![]() ,其中正确结论的个数是
,其中正确结论的个数是![]()

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
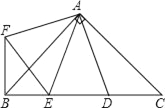
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①∠EAF=45°;②△AED≌△AEF;③△ABE∽△ACD;④BE2+DC2=DE2.
其中正确的是______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让同学们了解自己的体育水平,八年级1班的体育老师对全班50名学生进行了一次体育模拟测试(得分均为整数).成绩满分为10分,1班的体育委员根据这次测试成绩制作了如下的统计图:

(1)根据统计图所给的信息填写下表:
平均数(分) | 中位数(分) | 众数(分) | |
男生 | 8 | ||
女生 | 8 | 8 |
(2)若女生队测试成绩的方差为1.76,请计算男生队测试成绩的方差.并说明在这次体育测试中,哪个队的测试成绩更整齐些?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=6cm,BC=18cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.


(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中.
①已知点P的速度为每秒10cm,点Q的速度为每秒6cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为x、y(单位:cm,xy≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求x与y满足的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办的八年级学生数学素养大赛共设![]() 个项目:七巧板拼图,趣题巧解,数学应用,每个项目得分都按一定百分比折算后计入总分,总分高的获胜,下表为小米和小麦两位同学的得分情况(单位:分):
个项目:七巧板拼图,趣题巧解,数学应用,每个项目得分都按一定百分比折算后计入总分,总分高的获胜,下表为小米和小麦两位同学的得分情况(单位:分):
七巧板拼图 | 趣题巧解 | 数学应用 | |
小米 |
|
|
|
小麦 |
|
|
|
![]() 若七巧板拼图,趣题巧解,数学应用三项得分分别
若七巧板拼图,趣题巧解,数学应用三项得分分别![]() 按折算计入总分,最终谁能获胜?
按折算计入总分,最终谁能获胜?
![]() 若七巧板拼图按
若七巧板拼图按![]() 折算,小麦 (填“可能”或“不可能”)获胜.
折算,小麦 (填“可能”或“不可能”)获胜.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com