【题目】某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利80元．为了扩大销售、尽快减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价5元，商场平均每天就能多售出2件．请解答下列问题：
（1）当每件衬衫降价30元时，求商场每天销售该衬衫所获得的总利润．
（2）当该衬衫每件降价多少元时，商场销售该衬衫每天所获得的利润为1680元．
【答案】（1）当每件衬衫降价30元时，商场每天销售该衬衫所获得的总利润为1600元；（2）当该衬衫每件降价20元时，商场销售该衬衫每天所获得的利润为1680元
【解析】
（1）根据“总利润=单件的利润×件数”即可求出结论；
（2）设该衬衫每件降价x元，根据“总利润=单件的利润×件数”，列出一元二次方程即可求出结论．
解：（1）由题意可得总利润=（80－30）×（20＋
×2）=1600（元）
答：当每件衬衫降价30元时，商场每天销售该衬衫所获得的总利润为1600元．
（2）设该衬衫每件降价x元
由题意可知（80－x）×（20＋
×2）=1680
解得：
，
∵尽快减少库存，
∴
，
答：当该衬衫每件降价20元时，商场销售该衬衫每天所获得的利润为1680元．
科目：初中数学 来源： 题型：
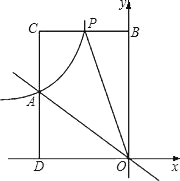
【题目】如图所示，正比例函数y＝kx与反比例函数
的图象交于点A（﹣3，2）．
（1）试确定上述正比例函数与反比例函数的解析式；
（2）根据图象回答，在第二象限内，当x取何值时，反比例函数的值大于正比例函数的值？
（3）P（m，n）是反比例函数图象上的一动点，其中﹣3＜m＜0，过点P作直线PB∥x轴，交y轴于点B，过点A作直线AD∥y轴，交x轴于点D，交直线PB于点C．当四边形OACP的面积为6时，请判断线段BP与CP的大小关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线y=kx+b交x轴于点A，交y轴于点B，直线y=2x﹣4交x轴于点D，与直线AB相交于点C（3，2）．
（1）根据图象，写出关于x的不等式2x﹣4＞kx+b的解集；
（2）若点A的坐标为（5，0），求直线AB的解析式；
（3）在（2）的条件下，求四边形BODC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某一项工程，在工程招标时，接到甲、乙两个工程队的投标书，施工一天，需付甲工程队工程款1.5万元，乙工程队工程款1.1万元，工程领导小组根据甲乙两队的投标书测算，可有三种施工方案：
（1）甲队单独完成这项工程刚好如期完成；
（2）乙队单独完成这项工程要比规定日期多用5天；
（3）若甲、乙两队合作4天，余下的工程由乙队单独也正好如期完成．
据上述条件解决下列问题：
①规定期限是多少天？写出解答过程；
②在不耽误工期的情况下，你觉得那一种施工方案最节省工程款?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，对角线AC,BD相交于O点，点P是线段AD上一动点（不与点D重合），PO的延长线交BC于Q点．
（1）求证：四边形PBQD为平行四边形.
（2）若AB=3cm，AD=4cm，P从点A出发．以1cm/s的速度向点D匀速运动．设点P的运动时间为ts，问：四边形PBQD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
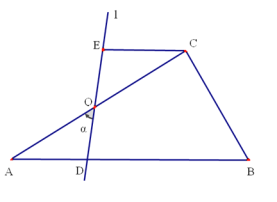
【题目】如图，在
中，
，
，
．点O是
的中点，过点O的直线
与从重合的位置开始，绕点O作逆时针旋转，交
于点D，过点Ｃ作
交直线于点Ｅ，设直线的旋转角为
．
（1）当四边形
是等腰梯形时，则=_______，此时
________；
（2）当四边形是直角梯形时，则=_________，此时_________；
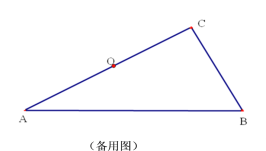
（3）当为几度时，判断四边形是否为菱形，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
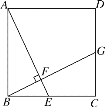
【题目】如图，在正方形ABCD中，点E在边BC上(点E不与点B重合)，连接AE，过点B作BF⊥AE于点F，交CD于点G.
(1)求证：△ABF∽△BGC；
(2)若AB＝2，G是CD的中点，求AF的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
