
【题目】已知,矩形ABCD中,AB=6cm,BC=18cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.


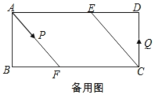
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
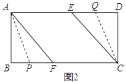
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中.
①已知点P的速度为每秒10cm,点Q的速度为每秒6cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为x、y(单位:cm,xy≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求x与y满足的函数关系式.
【答案】(1)证明见解析,![]() ;(2)①
;(2)①![]() ,②
,②![]() .
.
【解析】
(1)首先证明![]() ,由此得出
,由此得出![]() ,从而证明四边形
,从而证明四边形![]() 为菱形,然后在Rt△ABF中利用勾股定理进一步求解即可;
为菱形,然后在Rt△ABF中利用勾股定理进一步求解即可;
(2)①根据题意依次发现当![]() 点在
点在![]() 上时,
上时,![]() 点在
点在![]() 上以及
上以及![]() 点在
点在![]() 上时,
上时,![]() 点在
点在![]() 或
或![]() 上,也不能构成平行四边形,当
上,也不能构成平行四边形,当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时,才能构成平行四边形,据此进一步求解即可;②以
上时,才能构成平行四边形,据此进一步求解即可;②以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,根据题意分当
四点为顶点的四边形是平行四边形时,根据题意分当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时或当
上时或当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时以及当
上时以及当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时三种情况进一步分析求解即可.
上时三种情况进一步分析求解即可.
(1)证明:∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,
∴![]() ,
,
在![]() 和△COF中,
和△COF中,
∵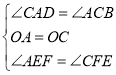
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
又∵![]() ,
,
∴四边形![]() 为菱形,
为菱形,
设菱形的边长![]() ,则
,则![]()
在Rt△ABF中,![]() ,
,
解得:![]() ,
,
∴![]() ;
;
(2)①显然当![]() 点在
点在![]() 上时,
上时,![]() 点在
点在![]() 上,此时
上,此时![]() 、
、![]() 、
、![]() 、
、![]() 四点不可能构成平行四边形;
四点不可能构成平行四边形;
同理![]() 点在
点在![]() 上时,
上时,![]() 点在
点在![]() 或
或![]() 上,也不能构成平行四边形.因此只有当
上,也不能构成平行四边形.因此只有当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时,才能构成平行四边形.
上时,才能构成平行四边形.
∴以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,![]() ,
,
∵点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,运动时间为
,运动时间为![]() 秒,
秒,
∴![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,![]() ;
;
②由题意得,以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,点
四点为顶点的四边形是平行四边形时,点![]() 、
、![]() 在互相平行的对应边上.
在互相平行的对应边上.
分三种情况:
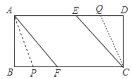
其一:如图1,当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时,
上时,![]() ,
,![]() ,即
,即![]() ;
;
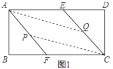
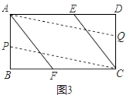
其二:如图2,当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时,
上时,![]() ,
,![]() ,即
,即![]() ;
;
其三:如图3,当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时,
上时,![]() ,
,![]() ,即
,即![]() ,
,
综上所述,![]() 与
与![]() 满足的函数关系式是
满足的函数关系式是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线y=kx+b交x轴于点A,交y轴于点B,直线y=2x﹣4交x轴于点D,与直线AB相交于点C(3,2).
(1)根据图象,写出关于x的不等式2x﹣4>kx+b的解集;
(2)若点A的坐标为(5,0),求直线AB的解析式;
(3)在(2)的条件下,求四边形BODC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
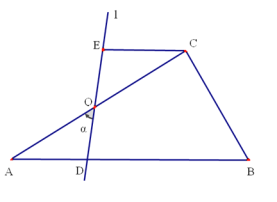
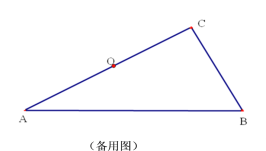
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点O是
.点O是![]() 的中点,过点O的直线
的中点,过点O的直线![]() 与从
与从![]() 重合的位置开始,绕点O作逆时针旋转,交
重合的位置开始,绕点O作逆时针旋转,交![]() 于点D,过点C作
于点D,过点C作![]() 交直线
交直线![]() 于点E,设直线
于点E,设直线![]() 的旋转角为
的旋转角为![]() .
.
(1)当四边形![]() 是等腰梯形时,则
是等腰梯形时,则![]() =_______,此时
=_______,此时![]() ________;
________;
(2)当四边形![]() 是直角梯形时,则
是直角梯形时,则![]() =_________,此时
=_________,此时![]() _________;
_________;
(3)当![]() 为几度时,判断四边形
为几度时,判断四边形![]() 是否为菱形,并说明理由.
是否为菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
(1)若CE=8,CF=6,求OC的长;
(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家体育用品商店出售同样的乒乓球和乒乓拍,乒乓球拍每幅定价20元,乒乓球每盒定价5元,现两家商店搞促销活动.甲店:每买一副球拍送一盒乒乓球;乙店:按定价的8折优惠.某班级需购球拍4副,乒乓球若干盒(不少于4盒).
(1)设购买乒乓球盒数为![]() (盒),在甲店购买的付款数为
(盒),在甲店购买的付款数为![]() (元);在乙店购买的付款数为
(元);在乙店购买的付款数为![]() (元),分别写出
(元),分别写出![]() 和
和![]() 与
与![]() 的函数关系式,并写出定义域.
的函数关系式,并写出定义域.
(2)就乒乓球的盒数讨论去哪家购买合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
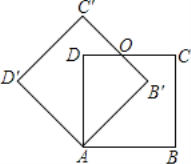
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转![]() 后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的面积是_________.
后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的面积是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
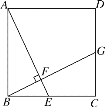
【题目】如图,在正方形ABCD中,点E在边BC上(点E不与点B重合),连接AE,过点B作BF⊥AE于点F,交CD于点G.
(1)求证:△ABF∽△BGC;
(2)若AB=2,G是CD的中点,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
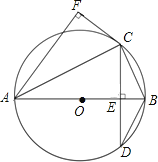
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com