
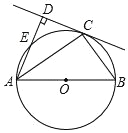
【题目】如图,AB 为⊙O 的直径,点 C 为⊙O 上一点,AD 和过点 C 的切线相互垂直,垂足为 D.
(1)求证:AC 平分∠DAB;
(2)AD 交⊙O 于点 E,若 AD=3CD=9,求 AE 的长度.
【答案】(1)见解析:(2)8.
【解析】
(1) 连接OC,根据AB为⊙0的直径, CD为⊙0的的切线可得AD//OC, 根据两直线平行, 内错角相等可得∠CAD=∠ACO,即可由∠OAC=∠ACO得到∠CAD=∠OAC, 即可得证AC平分∠DAB.
(2) 连接CE, 易证得△CDE∽△ADC,可得![]() =
=![]() ,即
,即 ![]() =
=![]() , 解得,DE=1,可得AE的长.
, 解得,DE=1,可得AE的长.
证明:(1)连接 OC,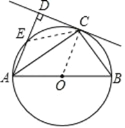
∵CD 是⊙ O 的切线,
∴OC⊥CD,又 AD⊥CD,
∴AD∥CO,
∴∠CAD=∠ACO,
∵OA=OC,
∴∠OAC=∠ACO,
∴∠CAD=∠OAC,即 AC 平分∠DAB;
(2)连接 EC,
由弦切角定理得,∠CAD=∠ECD,又∠ADC=∠CDE=90°,
∴△CDE∽△ADC,
∴![]() =
=![]() ,即
,即 ![]() =
=![]() , 解得,DE=1,
, 解得,DE=1,
∴AE=8.


科目:初中数学 来源: 题型:
【题目】某校举办的八年级学生数学素养大赛共设![]() 个项目:七巧板拼图,趣题巧解,数学应用,每个项目得分都按一定百分比折算后计入总分,总分高的获胜,下表为小米和小麦两位同学的得分情况(单位:分):
个项目:七巧板拼图,趣题巧解,数学应用,每个项目得分都按一定百分比折算后计入总分,总分高的获胜,下表为小米和小麦两位同学的得分情况(单位:分):
七巧板拼图 | 趣题巧解 | 数学应用 | |
小米 |
|
|
|
小麦 |
|
|
|
![]() 若七巧板拼图,趣题巧解,数学应用三项得分分别
若七巧板拼图,趣题巧解,数学应用三项得分分别![]() 按折算计入总分,最终谁能获胜?
按折算计入总分,最终谁能获胜?
![]() 若七巧板拼图按
若七巧板拼图按![]() 折算,小麦 (填“可能”或“不可能”)获胜.
折算,小麦 (填“可能”或“不可能”)获胜.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c(a≠0),过(1,y1)(2,y2).
①若 y1>0 时,则 a+b+c>0
②若 a=b 时,则 y1<y2
③若 y1<0,y2>0,且 a+b<0,则 a>0
④若 b=2a﹣1,c=a﹣3,且 y1>0,则抛物线的顶点一定在第三象限上述四个判断正确的有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
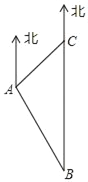
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向10(1+![]() )海里的C处,为了防止某国海巡警干扰,请求我A处的渔监船前往C处护航.如图,已知C位于A处的东北方向上,A位于B的北偏西30°方向上,则A和C之间的距离为( )
)海里的C处,为了防止某国海巡警干扰,请求我A处的渔监船前往C处护航.如图,已知C位于A处的东北方向上,A位于B的北偏西30°方向上,则A和C之间的距离为( )
A. 10![]() 海里 B. 20
海里 B. 20![]() 海里 C. 20
海里 C. 20![]() 海里 D. 10
海里 D. 10![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
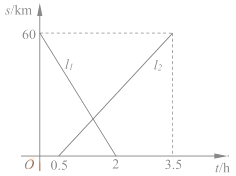
【题目】A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
(1)表示乙离开A地的距离与时间关系的图像是________(填![]() );
);
甲的速度是__________km/h;乙的速度是________km/h。
(2)甲出发后多少时间两人恰好相距5km?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com