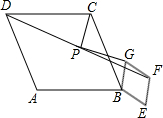
解:(1)延长GP交DC于H,
∵DC∥GF,
∴∠DHP=∠PGF,∠DPH=∠GPF,
∵DP=PF,
∴△DHP≌△PGF,

∴HD=GF,
∵四边形ABCD和四边形GFEB是菱形,
∴DC=CB,FG=GB,
∴DH=GB,
∴DC-DH=CB-GB,
∴CH=CG,
∴△CHG就是等腰三角形且CP是底边上的中线,根据等腰三角形三线合一的特点,
即可得出CP⊥PG;
∴线段PG与PC的位置关系是PG⊥PC;
(2)线段PG与PC的位置关系是PG⊥PC;
证明:如图②,延长GP到H,使PH=PG,
连接CH,CG,DH,
∵P是线段DF的中点,
∴FP=DP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP,
∴GF=HD,∠GFP=∠HDP,
∵
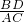
=
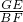
=

,
∴∠ADC=∠ABC=60°,∠GBF=60°,
∵四边形ABCD是菱形,
∴CD=CB,∠ADC=∠ABC=60°,点A、B、F又在一条直线上,
∴∠FBC=120°,
∴∠HDC=∠CBG=60°,
∵四边形BEFG是菱形,
∴GF=GB,
∴HD=GB,
即在△HDC与△GBC中,
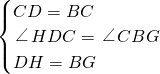
,
∴△HDC≌△GBC(SAS),
∴CH=CG,∠DCH=∠BCG,
∴∠DCH+∠HCB=∠BCG+∠HCB=120°,
即∠HCG=120°
∵CH=CG,PH=PG,
∴PG⊥PC.
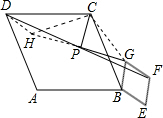
(3)将图①中的菱形BEFG饶点B顺时针旋转任意角度,
(1)中的结论没有变化,PG⊥PC.
分析:(1)可通过构建全等三角形求解.延长GP交DC于H,可证△DHP和△PGF全等,已知的有DC∥GF,根据平行线间的内错角相等可得出两三角形中两组对应的角相等,又有DP=PF,因此构成了全等三角形判定条件中的(AAS),得出两三角形全等,于是△CHG就是等腰直角三角形且CP是底边上的中线,根据等腰三角形三线合一的特点,即可得出CP⊥PG;
(2)方法同(1),只不过△CHG是个等腰三角形,得出顶角为120°,可根据三角函数来得出PG、CP的比例关系;
(3)经过(1)(2)的解题过程,我们要构建出以CP为底边中线的等腰三角形,那么可延长GP到H,使PH=PG,连接CH、DH,那么根据前两问的解题过程,我们要求的是三角形CHG是个等腰三角形,关键是证△GFP≌△HDP,根据已知得出△HDC≌△GBC,然后得出即可.
点评:此题主要考查了正方形,菱形的性质,以及全等三角形的判定等知识点,根据已知和所求的条件正确的构建出相关的全等三角形是解题的关键.

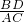 =
=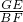 =
= .
.

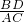 =
=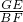 =
= ,
,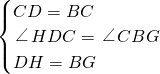 ,
,



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案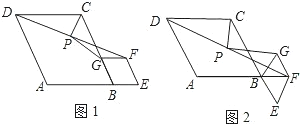 原问题中的其他条件不变,请你直接写出
原问题中的其他条件不变,请你直接写出


