
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( ) 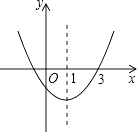
A.abc<0
B.2a+b<0
C.a﹣b+c<0
D.4ac﹣b2<0
【答案】D
【解析】解:A、根据图示知,抛物线开口方向向上,则a>0. 抛物线的对称轴x=﹣ ![]() =1>0,则b<0.
=1>0,则b<0.
抛物线与y轴交与负半轴,则c<0,
所以abc>0.
故A选项错误;
B、∵x=﹣ ![]() =1,
=1,
∴b=﹣2a,
∴2a+b=0.
故B选项错误;
C、∵对称轴为直线x=1,图象经过(3,0),
∴该抛物线与x轴的另一交点的坐标是(﹣1,0),
∴当x=﹣1时,y=0,即a﹣b+c=0.
故C选项错误;
D、根据图示知,该抛物线与x轴有两个不同的交点,则△=b2﹣4ac>0,则4ac﹣b2<0.
故D选项正确;
故选D.
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.


科目:初中数学 来源: 题型:
【题目】如图,小敏家厨房一墙角处有一自来水管,装修时为了美观,准备用木板从AB处将水管密封起来,互相垂直的两墙面与水管分别相切于D,E两点,经测量AD=10cm,BE=15cm, 则该自来水管的半径为( )cm.
A.5
B.10
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC=(填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,其斜坡CD坡比为1: ![]() ,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°. 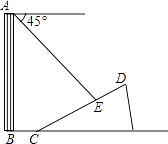
(1)求点E距水平面BC的高度;
(2)求楼房AB的高.(结果精确到0.1米,参考数据 ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC,∠C=90°,点D为AB上的一点,以AD为直径的⊙O与BC相切于点E,连接AE. 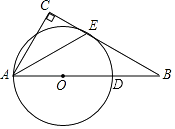
(1)求证:AE平分∠BAC;
(2)若AC=8,OB=18,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点. 
(1)求证:CF为⊙O的切线;
(2)当BF=5,sinF= ![]() 时,求BD的长.
时,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com