
分析 根据等边三角形的面积即可计算(h1-h2+h3)是等边三角形ABC的高,根据等边三角形的高即可求得BC的值,即可求得△ABC的面积,即可解题.
解答  解:设等边△ABC的边长为a,连接PA、PB、PC,
解:设等边△ABC的边长为a,连接PA、PB、PC,
则S△PAB+S△PBC-S△PAC=S△ABC,
从而$\frac{1}{2}$ah1-$\frac{1}{2}$ah2+$\frac{1}{2}$ah3=$\frac{\sqrt{3}}{4}$a2,
即 $\frac{1}{2}$a(h1-h2+h3)=$\frac{\sqrt{3}}{4}$a2,
∵h1-h2+h3=6,
∴a=4$\sqrt{3}$,
∴S△ABC=$\frac{\sqrt{3}}{4}$a2=12$\sqrt{3}$.
故答案为12$\sqrt{3}$.
点评 本题主要考查了等边三角形面积的计算,等边三角形高线长与边长的关系,本题中根据等边三角形的高计算等边三角形的面积是解题的关键.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:解答题
| 甲仓库 | 乙仓库 | |
| A工地 | x | 70-x |
| B工地 | 100-x | x+10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠B=90°,∠A=60°,AB=1,作等腰三角形△ACD,使∠CAD=30°,且点D和B位于AC异侧,连结BD交AC于点O
如图,在△ABC中,∠B=90°,∠A=60°,AB=1,作等腰三角形△ACD,使∠CAD=30°,且点D和B位于AC异侧,连结BD交AC于点O查看答案和解析>>
科目:初中数学 来源: 题型:填空题
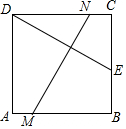 如图,将边长为8厘米的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段MN的长是4$\sqrt{5}$cm.
如图,将边长为8厘米的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段MN的长是4$\sqrt{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,在Rt△ABC中,AC=6,BC=8,D边AB上一点,连接CD,过点D作DE⊥DC交BC于E,把△BDE沿DE翻折得△DEB1,连接B1C.
已知,如图,在Rt△ABC中,AC=6,BC=8,D边AB上一点,连接CD,过点D作DE⊥DC交BC于E,把△BDE沿DE翻折得△DEB1,连接B1C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,抛物线y=-x2+20的图象与y轴正半轴的交点为A,将线段OA分成20等份,设分点分别为P1,P2,…,P19,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…,记△OP1Q1,△P1P2Q2,…的面积分别为S1,S2,…,S19,则S12+S22+…+S192的值为( )
如图,抛物线y=-x2+20的图象与y轴正半轴的交点为A,将线段OA分成20等份,设分点分别为P1,P2,…,P19,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…,记△OP1Q1,△P1P2Q2,…的面积分别为S1,S2,…,S19,则S12+S22+…+S192的值为( )| A. | 47 | B. | 47.5 | C. | 48 | D. | 48.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
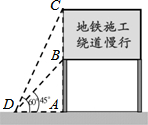 某市备受关注的地铁六号线正紧张施工,为了缓解一些施工路段交通拥挤的现状,交警队设立了如图所示的交通略况显示牌,已知立杆AB的高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°,求路况显示牌BC的高度.
某市备受关注的地铁六号线正紧张施工,为了缓解一些施工路段交通拥挤的现状,交警队设立了如图所示的交通略况显示牌,已知立杆AB的高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°,求路况显示牌BC的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,以O为端点画六条射线:OA,OB,OC,OD,OE,OF,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,…,那么按图中规律,所描的第59个点在射线OE上,第2017个点在射线OA上.
如图所示,以O为端点画六条射线:OA,OB,OC,OD,OE,OF,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,…,那么按图中规律,所描的第59个点在射线OE上,第2017个点在射线OA上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
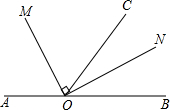 如图,点O为直线AB上一点,∠AOC=110°,OM平分∠AOC,∠MON=90°
如图,点O为直线AB上一点,∠AOC=110°,OM平分∠AOC,∠MON=90°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com