
 如图所示,以O为端点画六条射线:OA,OB,OC,OD,OE,OF,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,…,那么按图中规律,所描的第59个点在射线OE上,第2017个点在射线OA上.
如图所示,以O为端点画六条射线:OA,OB,OC,OD,OE,OF,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,…,那么按图中规律,所描的第59个点在射线OE上,第2017个点在射线OA上. 分析 根据1在射线OA上,2在射线OB上,3在射线OC上,4在射线OD上,5在射线OE上,6在射线OF上,7在射线OA上,…得出每6个数为一周期.用2017除以6,根据余数来决定数2017在哪条射线上.
解答 解:∵1在射线OA上,
2在射线OB上,
3在射线OC上,
4在射线OD上,
5在射线OE上,
6在射线OF上,
7在射线OA上,
…
每六个一循环,
59÷6=9…5,
2017÷6=336…1,
∴所描的第59个点在射线和5所在射线一样
所描的第2017个点在射线和1所在射线一样,
∴所描59个点在射线OE上,第2013个点在射线OA上.
故答案为:OE,OA.
点评 此题主要考查了数字变化规律,根据数的循环规律决定数的位置是解题关键.


科目:初中数学 来源: 题型:选择题
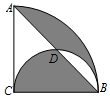 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )| A. | π-1 | B. | 2π-1 | C. | 2π-2 | D. | π-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 80-x=30%×(180+x) | B. | 80-x=30%×180 | C. | 180+x=30%×(80-x) | D. | 80-x=30%×260 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图,直线AB、CD、EF相交于点O,且AB⊥CD,OG平分∠BOE,如果∠EOG=$\frac{7}{22}$∠AOE,求∠EOG和∠DOF的度数.
(1)如图,直线AB、CD、EF相交于点O,且AB⊥CD,OG平分∠BOE,如果∠EOG=$\frac{7}{22}$∠AOE,求∠EOG和∠DOF的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
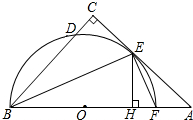 如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com