
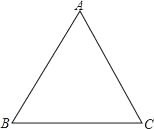
【题目】已知如图是边长为10的等边△ABC.
(1)作图:在三角形ABC中找一点P,连接PA、PB、PC,使△PAB、△PBC、△PAC面积相等.(不写作法,保留痕迹.)
(2)求点P到三边的距离和PA的长.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
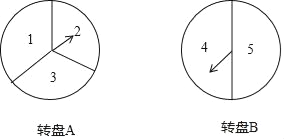
【题目】如图有两个可以自由转动的均匀转盘,A,B两个转盘被分成几个面积相等的扇形,并且在每个扇形内标上数字,转动转盘后,如果指针指在分割线上,那么重转一次,直到指针指向某一个扇形内为止.
(1)只转动A转盘,转盘停止后指针指向数字2的概率.
(2)如果同时转动A,B两个转盘,转盘停止后,将两个指针所指的数字相加,那么和是偶数的概率是多少,用树形图或表格说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
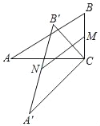
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,N是A'B'的中点,连接MN,若BC=4,∠ABC=60°,则线段MN的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
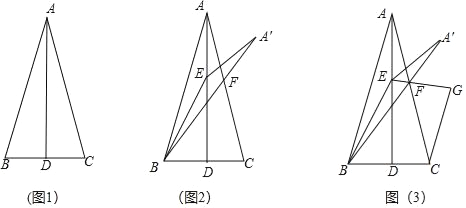
【题目】已知:AD是△ABC的高,且BD=CD.
(1)如图1,求证:∠BAD=∠CAD;
(2)如图2,点E在AD上,连接BE,将△ABE沿BE折叠得到△A′BE,A′B与AC相交于点F,若BE=BC,求∠BFC的大小;
(3)如图3,在(2)的条件下,连接EF,过点C作CG⊥EF,交EF的延长线于点G,若BF=10,EG=6,求线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
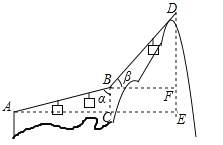
【题目】(2017安徽省)如图,游客在点A处做缆车出发,沿A﹣B﹣D的路线可至山顶D处,假设AB和BD都是直线段,且AB=BD=600m,α=75°,β=45°,求DE的长.
(参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花圃销售一批名贵花卉,平均每天可售出20盆,每盆盈利40元,为了增加盈利并尽快减少库存,花圃决定采取适当的降价措施,经调查发现,如果每盆花卉每降1元,花圃平均每天可多售出2盆.
(1)若花圃平均每天要盈利1200元,每盆花卉应降价多少元?
(2)每盆花卉降低多少元时,花圃平均每天盈利最多,是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在环境创优活动中,某居民小区要在一块靠墙(墙长25米)的空地上修建一个矩形养鸡场,养鸡场的一边靠墙,如果用60m长的篱笆围成中间有一道篱笆的养鸡场,设养鸡场平行于墙的一边BC的长为x(m),养鸡场的面积为y(m2)
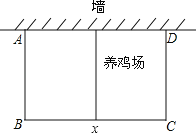
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)养鸡场的面积能达到300m2吗?若能,求出此时x的值,若不能,说明理由;
(3)根据(1)中求得的函数关系式,判断当x取何值时,养鸡场的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
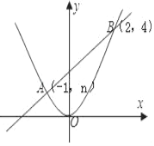
【题目】如图,一次函数y1=kx+b与二次函数y2=ax2的图象交于A(﹣1,n),B(2,4)两点.
(1)利用图中条件,求两个函数的解析式;
(2)根据图象直接写出使y1<y2的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com