
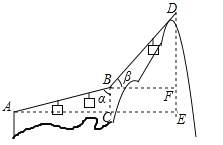
【题目】(2017安徽省)如图,游客在点A处做缆车出发,沿A﹣B﹣D的路线可至山顶D处,假设AB和BD都是直线段,且AB=BD=600m,α=75°,β=45°,求DE的长.
(参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.41)
≈1.41)
科目:初中数学 来源: 题型:
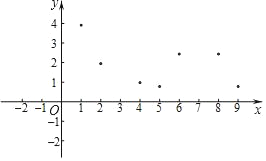
【题目】已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.
x | … | 1 | 2 | 4 | 5 | 6 | 8 | 9 | … |
y | … | 3.92 | 1.95 | 0.98 | 0.78 | 2.44 | 2.44 | 0.78 | … |
小风根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象和性质进行了探究.
下面是小风的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=7对应的函数值y约为多少;
②写出该函数的一条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
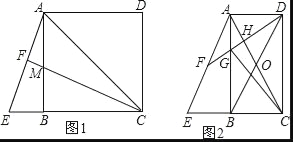
【题目】已知四边形ABCD是矩形,连接AC,点E是边CB延长线上一点,CA=CE,连接AE,F是线段AE的中点,
(1)如图1,当AD=DC时,连接CF交AB于M,求证:BM=BE;
(2)如图2,连接BD交AC于O,连接DF分别交AB、AC于G、H,连接GC,若∠FDB=30°,S四边形GBOH=![]() ,求线段GC的长.
,求线段GC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂每天生产![]() 、
、![]() 两种品牌的服装共600件,
两种品牌的服装共600件,![]() 、
、![]() 两种品牌的服装每件的成本和利润如右表:
两种品牌的服装每件的成本和利润如右表:
A | B | |
成本(元/件) | 50 | 35 |
利润(元/件) | 20 | 15 |
设每天生产![]() 种品牌服装
种品牌服装![]() 件,每天两种服装获利
件,每天两种服装获利![]() 元.
元.
(1)请写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果服装厂每天至少投入成本26400元,那么每天至少获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点C开始沿射线CA方向以1cm/s的速度运动;同时,点Q也从点C开始沿射线CB方向以3cm/s的速度运动.
(1)几秒后△PCQ的面积为3cm2?此时PQ的长是多少?(结果用最简二次根式表示)
(2)几秒后以A、B、P、Q为顶点的四边形的面积为22cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看![]() 次的人数没有标出).
次的人数没有标出).
根据上述信息,解答下列各题:
 ×
×
(1)该班级女生人数是__________,女生收看“两会”新闻次数的中位数是________;
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于![]() 次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低![]() ,试求该班级男生人数;
,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA、PB、AB、OP,已知PB是⊙O的切线.
(1)求证:∠PBA=∠C;
(2)若OP∥BC,且OP=9,⊙O的半径为3![]() ,求BC的长.
,求BC的长.
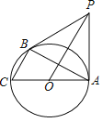
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com