
【题目】已知四边形ABCD是矩形,连接AC,点E是边CB延长线上一点,CA=CE,连接AE,F是线段AE的中点,
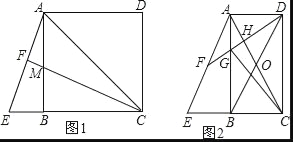
(1)如图1,当AD=DC时,连接CF交AB于M,求证:BM=BE;
(2)如图2,连接BD交AC于O,连接DF分别交AB、AC于G、H,连接GC,若∠FDB=30°,S四边形GBOH=![]() ,求线段GC的长.
,求线段GC的长.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)如图1,根据等腰三角形的三线合一得CF⊥AE,则∠AFC=90°,证明△AEB≌△CMB,可得BE=BM;
(2)如图2,作辅助线构建三角形全等,先证明△AMF≌△EBF,得FM=BF,AM=BE,再证明△DMB是等腰三角形,由三线合一得:DF平分∠BDM,根据∠FDB=30°得△BDM是等边三角形;由此△ACE为等边三角形,△OHD为直角三角形,设未知数:OH=x,根据S四边形GBOH=S△DGB-S△OHD,列方程得出结论.
详解:(1)如图1,∵AC=EC,F是AE的中点,
∴CF⊥AE,
∴∠AFC=90°,
∵四边形ABCD是矩形,AD=DC,
∴矩形ABCD为正方形,
∴AB=BC,∠ABC=90°,
∴∠AFC=∠ABC,
∵∠AMF=∠BMC,
∴∠EAB=∠MCB,
∵∠ABE=∠ABC=90°,
∴△AEB≌△CMB,
∴BE=BM;
(2)如图2,连接BF并延长交直线AD于M,
∵F是AE的中点,
∴AF=EF,
∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,
∴∠M=∠FBE,
∵∠AFM=∠EFB,
∴△AMF≌△EBF,
∴FM=BF,AM=BE,
∵AD=BC,
∴AD+AM=BC+BE,
即DM=CE,
∵AC=CE,
∴EC=DM=AC=BD,
∴△DMB是等腰三角形,
∵F是BM的中点,
∴DF平分∠BDM,
∵∠BDF=30°,
∴∠BDM=60°,
∴△BDM是等边三角形,
∴∠M=60°,
在Rt△BCD中,∠BDC=90°﹣60°=30°,
∴∠DBC=60°,
∵OB=OC,
∴∠DBC=∠OCB=60°,
∴△ACE为等边三角形,
在△OHD中,∠HOD=∠BOC=60°,
∴∠OHD=90°,
设OH=x,则OD=2x,BD=4x,BC=2x,
∴DH=![]() x,AH=x,DC=AB=2
x,AH=x,DC=AB=2![]() x,
x,
Rt△ABC中,∠ACE=60°,
∴∠BAC=30°,
∴cos30°=![]() ,
,
AG=![]() =
=![]() ,
,
∴BG=AB﹣AG=2![]() x﹣
x﹣![]() =
=![]() ,
,
∴S四边形GBOH=S△DGB﹣S△OHD,
=![]() BGAD﹣
BGAD﹣![]() OHDH,
OHDH,
=![]()
![]() 2x﹣
2x﹣![]() x
x![]() x=
x=![]() ,
,
解得:x2=9,
x=±3,
∴BC=2x=6,
BG=![]() ×3=4
×3=4![]() ,
,
由勾股定理得:CG=![]() =
=![]() =2
=2![]() .
.



 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
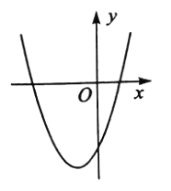
【题目】在平面直角坐标系中,二次函数![]() 的图象如图所示,点
的图象如图所示,点![]() ,
,![]() 是该二次函数图象上的两点,其中
是该二次函数图象上的两点,其中![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A. ![]() B.
B. ![]() C. 函数
C. 函数![]() 的最小值是
的最小值是![]() D. 函数
D. 函数![]() 的最小值是
的最小值是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2+mx+1,当0<x≤2时的函数值总是非负数,则实数m的取值范围为( )
A. m≥﹣2 B. ﹣4≤m≤﹣2 C. m≥﹣4 D. m≤﹣4或m≥﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
(1)求证:△ADE≌△CED;
(2)求证:DE∥AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )
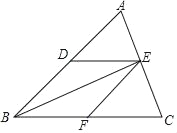
A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解某公司生产的100万只灯泡的使用寿命,可以采用抽样调查的方法
B. 4位同学的数学期末成绩分别为100、95、105、110,则这四位同学数学期末成绩的中位数为100
C. 甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的表现较甲更稳定
D. 某次抽奖活动中,中奖的概率为![]() 表示每抽奖50次就有一次中奖
表示每抽奖50次就有一次中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________
的坐标为__________
(2)在线段![]() 上有一点
上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 交直线
交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形.
是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
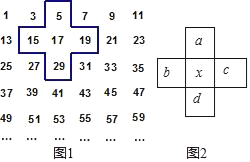
【题目】如图,将连续的奇数1,3,5,7…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
(1)若x=17,则a+b+c+d= .
(2)移动十字框,用x表示a+b+c+d= .
(3)设M=a+b+c+d+x,判断M的值能否等于2020,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com