
【题目】如图,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________
的坐标为__________
(2)在线段![]() 上有一点
上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 交直线
交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形.
是平行四边形.

【答案】(1)(8,0) , (0,4) ;(2)当m为![]() 时,四边形OBEF是平行四边形.
时,四边形OBEF是平行四边形.
【解析】
(1)由点C的坐标利用待定系数法即可求出直线![]() 的解析式,再分别令直线
的解析式,再分别令直线![]() 的解析式中x=0、y=0求出对应的y、x值,即可得出点A、B的坐标;
的解析式中x=0、y=0求出对应的y、x值,即可得出点A、B的坐标;
(2)由点C的坐标利用待定系数法即可求出直线![]() 的解析式,结合点E的横坐标即可得出点E、F的坐标,再根据平行四边形的性质即可得出关于m的一元一次方程,解方程即可得出结论;
的解析式,结合点E的横坐标即可得出点E、F的坐标,再根据平行四边形的性质即可得出关于m的一元一次方程,解方程即可得出结论;
解:(1)将点C(4,2)代入y=![]() x+b中,
x+b中,
得:2=2+b,解得:b=4,
∴直线![]() 为y=
为y=![]() x+4.
x+4.
令y=![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴B(0,4);
令y=![]() x+4中y=0,则x=8,
x+4中y=0,则x=8,
∴A(8,0).
故答案为:(8,0)(0,4)
(2)将C(4,2)分别代入y=-![]() x+b, y=kx-6,得b=4,k=2.
x+b, y=kx-6,得b=4,k=2.
∴直线l1的解析式为y=-![]() x+4,直线l2的解析式为y=2x-6.
x+4,直线l2的解析式为y=2x-6.
∵点E的横坐标为m,
∴点E的坐标为(m,-![]() m+4),点F的坐标为(m,2m-6).
m+4),点F的坐标为(m,2m-6).
∴EF=-![]() m+4-(2m-6)=-
m+4-(2m-6)=-![]() m+10.
m+10.
∵四边形OBEF是平行四边形,
∴EF=OB,即-![]() m+10=4.
m+10=4.
解得m=![]() .
.
∴当m为![]() 时,四边形OBEF是平行四边形.
时,四边形OBEF是平行四边形.


科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形纸片ABCD中,AB=2,BC=3.
操作:将矩形纸片沿EF折叠,使点B落在边CD上.
探究:(1)如图1,若点B与点D重合,你认为△EDA1和△FDC全等吗?如果全等,请给出证明,如果不全等,请说明理由;
(2)如图2,若点B与CD的中点重合,请你判断△FCB1、△B1DG和△EA1G之间的关系,如果全等,只需写出结果,如果相似,请写出结果和相应的相似比;
(3)如图2,请你探索,当点B落在CD边上何处,即B1C的长度为多少时,△FCB1与△B1DG全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数 1,3,5,7,9,…,排成如图的数阵.
(1)十字框中的五个数的和与中间数 15 有什么关系?
(2)设中间数为 a,用式子表示十字框中五个数之和;
(3)十字框中五个数之和能等于 2 005 吗?若能,请写出这五个数;若不能, 说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个二元一次方程ax+by=c(a,b,c,为常数,且A,B均不为0)有无数组解,我们规定,将其每一个解中x,y的值分别作为一个点的横,纵坐标极点在平面直角坐标系中,这样我们就得到了二元一次方程的图象:一条直线,既二元一次方程的解均满足其对应直线上点的坐标,反之直线上点的坐标均为其对应的二元一次方程的解,即2x-y=0,其中一解x=1,y=2,则对应其图象上一个点(1,2).
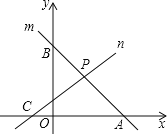
(1)如图,3x+3y=12,的图象为直线m,其与x轴交点A的坐标为____,其与y轴交点B的坐标为___;
(2)如图,ax+by=-5的图象为直线n,其与x轴交于C(-![]() ,0),与(1)中直线m交于P,若P的横坐标为1,求a和b的值.
,0),与(1)中直线m交于P,若P的横坐标为1,求a和b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)过以下三个点:(m,n),(m+2,2n),和(m+6,n),当抛物线上另有点的横坐标为m+4时,它的纵坐标为_____;当横坐标为m﹣2时,它的纵坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F,若小敏行走的路程为3100m,则小聪行走的路程为( )m.
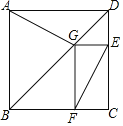
A.3100B.4600C.3000D.3600
查看答案和解析>>
科目:初中数学 来源: 题型:
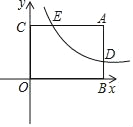
【题目】如图所示,已知矩形ABOC中,AC=4,双曲线y=![]() 与矩形两边AB、AC分别交于D、E,E为AC边中点.
与矩形两边AB、AC分别交于D、E,E为AC边中点.
(1)求点E的坐标;
(2)点P是线段OB上的一个动点,是否存在点P,使∠DPC=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
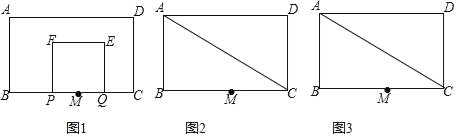
【题目】如图,在矩形ABCD中,AB=3,BC=4,点M是BC的中点,点P从点M出发沿MB以每秒1个单位的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;同时点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P,Q的运动过程中,以PQ为边作正方形PQEF,使它与矩形ABCD在BC的同侧,点P,Q同时出发,当点P返回点M时,则两点停止运动,设点P,Q运动的时间是t秒(t>0).
(1)当点P运动到BM的中点时,t= ;
(2)设正方形PQEF与矩形ABCD重叠部分的面积为S,直接写出S与t之间的函数关系式及t的取值范围;
(3)连结AC,当正方形PQEF与△ADC重叠部分为三角形时,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com