
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F,若小敏行走的路程为3100m,则小聪行走的路程为( )m.
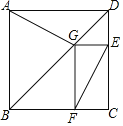
A.3100B.4600C.3000D.3600
【答案】B
【解析】
连接CG,由正方形的对称性,易知AG=CG,由正方形的对角线互相平分一组对角,GE⊥DC,易得DE=GE.在矩形GECF中,EF=CG.要计算小聪走的路程,只要得到小聪比小敏多走了多少就行.
连接GC,
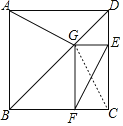
∵四边形ABCD为正方形,
所以AD=DC,∠ADB=∠CDB=45°,
∵∠CDB=45°,GE⊥DC,
∴△DEG是等腰直角三角形,
∴DE=GE.
在△AGD和△GDC中,
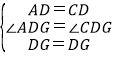 ,
,
∴△AGD≌△GDC(SAS)
∴AG=CG,
在矩形GECF中,EF=CG,
∴EF=AG.
∵BA+AD+DE+EF-BA-AG-GE,
=AD=1500m.
∵小敏共走了3100m,
∴小聪行走的路程为3100+1500=4600(m),
故选B.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】慢车和快车先后从甲地出发沿直线道路匀速驶向乙地,快车比慢车晚出发0.5小时,行驶一段时间后,快车途中体息,休息后继续按原速行驶,到达乙地后停止.慢车和快车离甲地的距离y(千米)与慢车行驶时间x(小时)之间的函数关系如图所示.
(1)直接写出快车速度是 千米/小时.
(2)求快车到达乙地比慢车到达乙地早了多少小时?
(3)求线段BC对应的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________
的坐标为__________
(2)在线段![]() 上有一点
上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 交直线
交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形.
是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +8 |
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
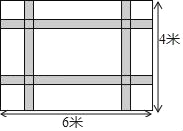
【题目】如图,一块长6米宽4米的地毯,为了美观设计了两横两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.(供参考数据:1052=11025,1152=13225,1252=15625)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A(0,4),C(2,0).

(1)三角形![]() 的面积= ;
的面积= ;
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿![]() 轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿
轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿![]() 轴正方向移动,点Q到达A点整个运动随之结束,AC的中点D的坐标是(1,2),设运动时间为
轴正方向移动,点Q到达A点整个运动随之结束,AC的中点D的坐标是(1,2),设运动时间为![]() 秒,问:是否存在这样的
秒,问:是否存在这样的![]() ,使
,使![]() 若存在,请求出的值;若不存在,请说明理由;
若存在,请求出的值;若不存在,请说明理由;
(3)如图2,点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF,点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,以下两个式子:![]() 哪个式子为定值,请求出这个定值.
哪个式子为定值,请求出这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )
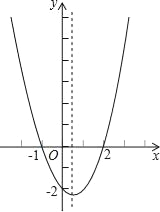
A. 函数有最小值 B. 对称轴是直线x=![]()
C. 当﹣1<x<2时,y<0 D. 当x>![]() 时,y随x的增大而增大
时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D,E分别是△ABC的边BA和BC延长线上的点,作∠DAC的平分线AF,若AF∥BC.

(1)求证:△ABC是等腰三角形;
(2)作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com