
����Ŀ����֪����ֽƬABCD�У�AB=2��BC=3��
������������ֽƬ��EF�۵���ʹ��B���ڱ�CD�ϣ�
̽������1����ͼ1������B���D�غϣ�����Ϊ��EDA1����FDCȫ�������ȫ�ȣ������֤���������ȫ�ȣ���˵�����ɣ�
��2����ͼ2������B��CD���е��غϣ������ж���FCB1����B1DG����EA1G֮��Ĺ�ϵ�����ȫ�ȣ�ֻ��д�������������ƣ���д���������Ӧ�����Ʊȣ�
��3����ͼ2������̽��������B����CD���Ϻδ�����B1C�ij���Ϊ����ʱ����FCB1����B1DGȫ�ȣ�

���𰸡���1��ȫ�ȣ���2����FCB1����B1DG���ƣ����Ʊ�Ϊ4��3����3����B1C=3��![]() ʱ����FCB1����B1DGȫ�ȣ�
ʱ����FCB1����B1DGȫ�ȣ�
�������������������1�����ݾ��ε����ʿɵ���A=��B=��C=��ADC=90����AB=CD��������A=��A1����B=��A1DF=90����CD=A1D������ͬ�ǵ������ȿɵ���A1DE=��CDF������֤�ý��ۣ�
��2����B1DG����EA1Gȫ��֤��ͬ��1������FC= ![]() ����B1F=BF=
����B1F=BF= ![]() ��B1C=
��B1C=![]() DC=1�����ݹ��ɶ��������з������x��ֵ���Ӷ������FCB1����B1DG���Ƶ����Ʊȣ�
DC=1�����ݹ��ɶ��������з������x��ֵ���Ӷ������FCB1����B1DG���Ƶ����Ʊȣ�
��3����![]() ������
������![]() ��
�� ![]() ����ֱ��
����ֱ��![]() �У����ݹ��ɶ����з�����⼴��.
�У����ݹ��ɶ����з�����⼴��.
��1��ȫ�ȣ�
���ı���ABCD�Ǿ��Σ�
������A=��B=��C=��ADC=90����AB=CD��
������֪����A=��A1����B=��A1DF=90����CD=A1D��
������A1=��C=90������CDF+��EDF=90����
������A1DE=��CDF��������EDA1�ա�FDC��ASA����
��2����B1DG����EA1Gȫ�ȣ�
��FCB1����B1DG���ƣ���FC= ![]() ����B1F=BF=
����B1F=BF= ![]() ��B1C=
��B1C=![]() DC=1��
DC=1��
����![]() ������
������![]() ��
��
������FCB1����B1DG���ƣ����Ʊ�Ϊ4��3��
��3����FCB1����B1DGȫ�ȣ���![]() ������
������![]() ��
�� ![]() ��
��
��ֱ��![]() �У��ɵ�
�У��ɵ�![]() ��
��
������![]() �����
�����![]() (��һ����ȥ)��
(��һ����ȥ)��
���ԣ���B1C=![]() ʱ����FCB1����B1DGȫ�ȣ�
ʱ����FCB1����B1DGȫ�ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �Ľ�ƽ���ߣ�����
�Ľ�ƽ���ߣ�����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ת��ʹ
��ת��ʹ![]() �����߽�ֱ��
�����߽�ֱ��![]() �ڵ�
�ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() �������������⣺
�������������⣺

(1)��![]() �Ƶ�
�Ƶ�![]() ��ת����ͼ1��λ�ã���
��ת����ͼ1��λ�ã���![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ���߶�
���߶�![]() ��ʱ��������
��ʱ��������![]() .
.
�����ж��߶�![]() ��
��![]() ��
��![]() ֮���������ϵ��������֤��
֮���������ϵ��������֤��
�����![]() �Ķ���.
�Ķ���.
(2)��![]() ���ֵ���(1)�ж������Ƶ�
���ֵ���(1)�ж������Ƶ�![]() ��ת��ͼ2��λ��ʱ����
��ת��ͼ2��λ��ʱ����![]() ��
��![]() ����
����![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ϳ쳵�Ⱥ�Ӽس�����ֱ�ߵ�·����ʻ���ҵأ��쳵������������0.5Сʱ����ʻһ��ʱ��쳵;����Ϣ����Ϣ�������ԭ����ʻ�������ҵغ�ֹͣ�������Ϳ쳵��صľ���y��ǧ�ף���������ʻʱ��x��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ��
��1��ֱ��д���쳵�ٶ����� ǧ��/Сʱ��
��2����쳵�����ҵر����������ҵ����˶���Сʱ��
��3�����߶�BC��Ӧ�ĺ�����ϵʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵĵ�A��ʾ����Ϊ6����B��ʾ����Ϊ-4����C��AB���е㣬����P�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊx�루x��0����
![]()
��1����x=5___��ʱ����P�����A��
��2���˶������е�P��ʾ������2x-4____���ú�x�Ĵ���ʽ��ʾ����
��3����P��C֮��ľ���Ϊ2����λ����ʱ����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������6������ʳ������Ķ������£���+����ʾ������-����ʾ���⣩
+25�� +8��-12��+34��-36��-22��
��1��������6�죬���������ʳ������Ǽ����ˣ�ͨ������˵����
��2��������6�죬�ֿ����Ա���㷢�ֿ��ﻹ��480��������ô6��ǰ����������ٶ֣�
��3�����������װж�Ѷ���ÿ��5Ԫ����ô��6��Ҫ������װж�ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�������������
-3��9��-27��81����
1��-3��9��-27����
-2��10��-26��82����
��1�����ڢ��������еĹ��ɣ���5������ ��
�۲�ڢ�������ڢ������Ĺ�ϵ���ڢ��е�n������ ���ú�n��ʽ�ӱ�ʾ��
�۲�ڢ�������ڢ������Ĺ�ϵ���ڢ��е�n������ ���ú�n��ʽ�ӱ�ʾ��
��2��ȡÿ�����ĵ�7�������������������ĺͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A����4��2����B��n����4��������һ�κ���y=kx+b�ͷ���������y=![]() ͼ����������㣮
ͼ����������㣮
��1����һ�κ����ͷ����������Ľ���ʽ��
��2������AOB�������
��3���۲�ͼ��ֱ��д������ʽkx+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �ֱ���
�ֱ���![]() �ᣬ
�ᣬ![]() �ύ��
�ύ��![]() ���㣬��ֱ��
���㣬��ֱ��![]() ���ڵ�
���ڵ�![]() .
.
��1����![]() ������Ϊ__________����
������Ϊ__________����![]() ������Ϊ__________
������Ϊ__________
��2�����߶�![]() ����һ��
����һ��![]() ������
������![]() ��
��![]() ���ƽ����
���ƽ����![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() Ϊ��ֵʱ���ı���
Ϊ��ֵʱ���ı���![]() ��ƽ���ı���.
��ƽ���ı���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0���Ĵ���ͼ����ͼ��ʾ�����ڸö��κ���������˵���д�����ǣ�������
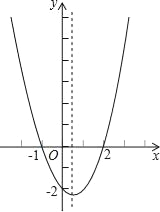
A. ��������Сֵ B. �Գ�����ֱ��x=![]()
C. ����1��x��2ʱ��y��0 D. ��x��![]() ʱ��y��x�����������
ʱ��y��x�����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com